Прикладная геометрия
| Реализация на С++ | |
Библиотеку с реализацией большей части этих функций можно найти на странице Библиотека myBasicGeometry | |
В этом разделе будут рассмотрены решения основных геометрических задач встречающихся при программировании роботов.
Содержание
Системы координат
Переход от одной системы координат к другой
Одна из наиболее распространенных геометрических задач, которые предстоит решать робототехнику - переход между системами координат. Чаще всего это нужно будет делать на плоскости, особенно при решении задач глобальной навигации. Типичная задача в робототехнике будет выглядеть так:
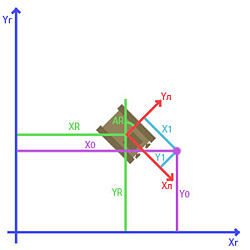
Робот находится в координатах (XR,YR) в глобальной системе координат (на карте) и повернут на угол AR по часовой стрелке от направления оси O-X, робот обнаружил препятствие относительно себя в координатах (X1,Y1) локальной системы координат робота. Требуется определить глобальные координаты (X0,Y0) препятствия. Либо наоборот - зная глобальные координаты препятствия требуется вычислить его локальные координаты.
Тройка чисел (XR,YR,AR) - координаты базиса локальной системы координат в глобальной системе координат.
| Формулы перевода из локальных координат в глобальные |
|---|
|
X0=XR+X1*cos(AR)-Y1*sin(AR) Y0=YR+Y1*cos(AR)+X1*sin(AR) |
| Формулы обратного перевода координат |
|
X1=(X0-XR)*cos(AR)+(Y0-YR)*sin(AR) Y1=(Y0-YR)*cos(AR)-(X0-XR)*sin(AR) |
Проверим: (переведем координаты туда и обратно)
X1=(X0-XR)*cos(AR)+(Y0-YR)*sin(AR)= =(XR+X1*cos(AR)-Y1*sin(AR)-XR)*cos(AR)+(YR+Y1*cos(AR)+X1*sin(AR)-YR)*sin(AR)= =(X1*cos(AR)-Y1*sin(AR))*cos(AR)+(Y1*cos(AR)+X1*sin(AR))*sin(AR)= =X1*cos(AR)*cos(AR)-Y1*sin(AR)*cos(AR)+Y1*cos(AR)*sin(AR)+X1*sin(AR)*sin(AR)= =X1*cos(AR)*cos(AR)+X1*sin(AR)*sin(AR)=X1*(cos(AR)*cos(AR)+sin(AR)*sin(AR))=X1*(1)=X1,
и вторую координату:
Y1=(Y0-YR)*cos(AR)-(X0-XR)*sin(AR)= =(YR+Y1*cos(AR)+X1*sin(AR)-YR)*cos(AR)-(XR+X1*cos(AR)-Y1*sin(AR)-XR)*sin(AR)= =(Y1*cos(AR)+X1*sin(AR))*cos(AR)-(X1*cos(AR)-Y1*sin(AR))*sin(AR)= =Y1*cos(AR)*cos(AR)+X1*sin(AR)*cos(AR)-X1*cos(AR)*sin(AR)+Y1*sin(AR)*sin(AR)= =Y1*cos(AR)*cos(AR)+Y1*sin(AR)*sin(AR)=Y1*(cos(AR)*cos(AR)+sin(AR)*sin(AR))=Y1*(1)=Y1.
Точки, прямые, отрезки и операции с ними
Общее уравнение прямой и получение его по двум точкам на прямой
Общее уравнение первой прямой на плоскости выглядит так:
A*x+B*y+C=0
Понятно, что при этом коэффициенты A,B,C задаются с точностью до умножения на ненулевое число. Если где-то нам потребуется однозначность, тогда мы можем дополнительно нормировать эту тройку до A^2+B^2+C^2=1 и тогда останется подобрать лишь знак (надо будет с этим что-то тоже сделать :)).
Теперь, если нам известны две различные точки на этой прямой (x1,y1) и (x2,y2), тогда мы можем выписать вариант этих коэффициентов как:
A=y1-y2, B=x2-x1, C=x1*y2-y1*x2
Далее если нам надо получить коэффициенты (A,B,C) для прямой определяемой отрезком (x1,y1)-(x2,y2), то мы будем пользоваться функцией (внутренность которой определена выше):
(A,B,C)=getLineCoefsFromTwoPoints(x1,y1,x2,y2)
Пересечение двух прямых
Пересечением двух прямых может быть точка, две прямые могут совпадать (тогда пересечение - любая из них) и они могут оказаться параллельны (тогда пересечение пусто).
Чтобы найти пересечение двух прямых A1*x+B1*y+C1=0 и A2*x+B2*y+C2=0 нужно рассмотреть эти два уровнения как систему и решить её.
Для этого найдем три специальные величины:
d=A1*B2-A2*B1 d1=C2*B1-B2*C1 d2=C1*A2-A1*C2
Теперь если d=0 тогда прямые параллельны и совпадают только если d1=d2=0.
А если же d<>0, тогда прямые пересекаются в точке:
x=d1/d y=d2/d
Принадлежность точки отрезку
Это достаточно простая проверка. Пусть точка имеет координаты (x,y), а отрезок (xa,ya)-(xb,yb). Тогда сначала найдем коэфициенты общего уравнения прямой, на которой лежит отрезок через определенную выше функцию (A,B,C)=getLineCoefsFromTwoPoints(xa,ya,xb,yb). Теперь, если не выполняется условие:
1) A*x+B*y+C=0
Значит точка не лежит на прямой, если же выполняется, то осталось проверить, что точка лежит внутри отрезка:
2) min(xa,xb)<=x<=max(xa,xb) 3) min(ya,yb)<=y<=max(ya,yb)
Теперь, если все три условия выполнены, тогда точка принадлежит отрезку.
Пересчение двух отрезков
Часто в робототехнике требуется определить пересекаются ли два отрезка, и если пересекаются, то в какой точке (или по какому отрезку). Например, это нужно для поиска путей на карте (проверяем пересечение пути робота с препятствиями заданными многоугольниками) или для вычисления расстояния до препятсвий (когда ищем точку пересечения луча ИК-дальномера с препятствием, нанесенным на карте и сравниваем с расстоянием, которое нам показывает дальномер).
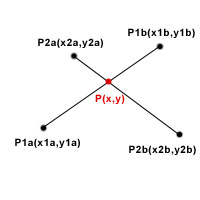
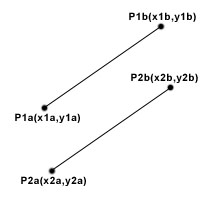
Постановка задачи: Даны два НЕВЫРОЖДЕННЫХ (то есть не являющихся точками) отрезка P1a(x1a,y1a)-P1b(x1b,y1b) и P2a(x2a,y2a)-P2b(x2b,y2b). Требуется определить, пересекаются ли эти два отрезка, если пересекаются, то в какой точке или по какому отрезку.
Решение:
В целом решение будет по следующей схеме:
- Определяем прямые, на которых лежат отрезки;
- Если прямые не параллельны, тогда находим точку их пересечения и проверяем, что она лежит на обоих отрезках;
- Если же прямые параллельны, тогда рассматриваем два варианта:
- Если прямые не совпадают, тогда общих точек нет
- Если прямые совпали, смотрим взаимное расположение отрезков и если они пересекаются, то выписываем, по какому отрезку.
Теперь подробно по каждому шагу:
Шаг 1.
Координаты точек каждого отрезка определяются формулами:
P1(u)=P1a+u*(P1b-P1a), где 0<=u<=1, P2(v)=P2a+v*(P2b-P2a), где 0<=v<=1,
Выпишем это в координатах:
x1(u)=x1a+u*(x1b-x1a) y1(u)=y1a+u*(y1b-y1a) x2(v)=x2a+v*(x2b-x2a) y2(v)=y2a+v*(y2b-y2a)
Нам требуется найти такие u,v, что:
x1(u)=x2(v) => x1a+u*(x1b-x1a)=x2a+v*(x2b-x2a) y1(u)=y2(v) => y1a+u*(y1b-y1a)=y2a+v*(y2b-y2a)
Это система из двух линейных уравнений с двумя неизвестными вида:
A1*u+B1*v+C1=0, где A1=x1b-x1a, B1=x2a-x2b, C1=x1a-x2a A2*u+B2*v+C2=0, где A2=y1b-y1a, B2=y2a-y2b, C2=y1a-y2a
Выпишем важную величину:
D=A1*B2-A2*B1
Она равна нулю, тогда и только тогда, когда прямые параллельны.
Шаг 2
Если прямые не параллелны (D<>0), тогда можно выписать решение системы как:
u=(B2*C1-C2*B1)/D v=(C1*A2-A1*C2)/D
Останется лишь проверить условие
0<=u<=1 и 0<=v<=1
чтобы убедится, что точка пересечения прямых принадлежит обоим отрезкам.
Шаг 3
Если же прямые параллельны (D=0), тогда нужно проверять совпадают ли они. Если выполняется условие
D1<>0 или D2<>0, где D1=A1*C2-A2*C1 и D2=B1*C2-B2*C1
тогда прямые не совпадают и общих точек у отрезков нет. Если же D1=D2=0, тогда прямые совпадают и нужно проверить накладываются ли отрезки. Для этого просто выпишем координаты концов второго отрезка в базисе соответствующему первому отрезку:
P2a=P1a+u2a*(P1b-P1a) => => u2a*(P1b-P1a)=P2a-P1a => => u2a*(P1b-P1a)*(P1b-P1a)=(P2a-P1a)*(P1b-P1a) => => u2a=((P2a-P1a)*(P1b-P1a))/((P1b-P1a)*(P1b-P1a))
Аналогично:
P2b=P1a+u2b*(P1b-P1a) => ... => u2b=((P2b-P1a)*(P1b-P1a))/((P1b-P1a)*(P1b-P1a))
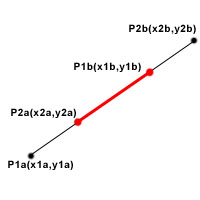
Теперь если max(u2a,u2b)<0 или min(u2a,u2b)>1 тогда отрезки общих точек не имеют, иначе они пересекаются по отрезку:
P1a+u*(P1b-P1a), где max(0,min(u2a,u2b))<u<min(1,max(u2a,u2b))
Всё.
Скалярное произведение векторов на плоскости
Одним из самых полезных понятий в вычислительной геометрии является скалярное произведение A*B векторов, которое для векторов A=(dx1,dy1) и B=(dx2,dy2) вычисляется по формуле dx1*dx2+dy1*dy2 и равно косинусу угла между векторами умноженному на их длины. Его полезно применять для проверки - направлены ли вектора в одну сторону или нет. А также если у нас есть перпендикулярные вектора X и Y, тогда можно любой вектор Z разложить в линейную комбинацию векторов X,Y по формуле Z=a*X+b*Y, где a=Z*X/|X|^2, b=Z*Y/|Y|^2.
Векторное произведение на плоскости
Другим полезным понятием в вычислительной геометрии является векторное произведение AxB на плоскости, равное ориентированной площади параллелограма натянутого на вектора A=(dx1,dy1) и B=(dx2,dy2). Вычисляется это число по формуле dy1*dx2-dy2*dx1, и равно синусу угла между векторами умноженному на их длины и позволяет определить направлен ли вектор (dx2,dy2) влево или вправо от вектора (dx1,dy1). Кроме того понятно, что модуль этого произведения деленный на 2 будет равен площади треугольника натянутого на эти вектора отложенные из одной точки.
Многоугольники, операции с ними
Пересечение отрезка с многоугольником
Для целей поиска пути на карте нам потребуется научиться определять - пересекает ли отрезок [SF] необязательно выпуклый многоугольник без самопересечений (причем в более тонком смысле, чем проверка на существование общих точек - нас будет интересовать принадлежность точек отрезка внутренним точкам многоугольника). Будем считать что многоугольник задан обходом его точек против часовой стрелки (то есть многоугольник всегда слева от границы при движении в порядке определения его точек).
Будем рассматривать каждую вершину многоугольника C вкупе с интервалом (P,C) до предыдущей вершины C, а также обозначим для удобства следующую его вершину после C как вершину N. Если пересечений отрезка [S,F] с полуинтервалом (P,C] нет (задача определения пересечения отрезков решается выше), тогда будем считать что в относительно вершины C нам рассматривать нечего и переходим дальше.
Теперь у нас будет два варианта - отрезок [S,F] пересекается с отрезком [P,C] в одной точке и эта точке не C, либо он пересекается с отрезком [P,C] по некоторому отрезку (очевидно что в этом случае он параллелен [P,C]):
Если пересечение в 1 точке и эта точка внутри интервала (P,C), тогда достаточно проверить, что ни точка S ни точка F не лежат слева от вектора PC (это легко сделать с помощью векторного произведения на плоскости - см. выше).
Если пересечение в 1 точке и эта точка С и вектор CN лежит левее вектора PC или параллелен ему, тогда надо проверить, что ни точка S ни точка F не лежат слева от одновременно CN и PC.
Если пересечение в 1 точке и эта точка С и вектор CN лежит правее вектора PC, тогда надо проверить, что ни точка S ни точка F не лежат слева от либо CN и PC.
Если же пересечение отрезок, тогда надо лишь проверить, что если вектор CN лежит правее вектора PC, тогда ни CS ни CF не направлены в ту же сторону, что и вектор PC (проверяется скалярным произведением).
Всё.