Прикладная геометрия
В этом разделе будут рассмотрены решения основных геометрических задач встречающихся при программировании роботов.
Содержание
Переход от одной системы координат к другой
Одна из наиболее распространенных геометрических задач, которые предстоит решать робототехнику - переход между системами координат. Чаще всего это нужно будет делать на плоскости, особенно при решении задач глобальной навигации. Типичная задача в робототехнике будет выглядеть так:
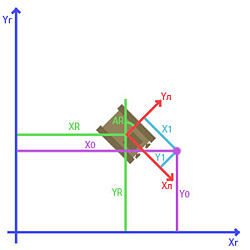
Робот находится в координатах (XR,YR) в глобальной системе координат (на карте) и повернут на угол AR по часовой стрелке от направления оси O-X, робот обнаружил препятствие относительно себя в координатах (X1,Y1) локальной системы координат робота. Требуется определить глобальные координаты (X0,Y0) препятствия. Либо наоборот - зная глобальные координаты препятствия требуется вычислить его локальные координаты.
Тройка чисел (XR,YR,AR) - координаты базиса локальной системы координат в глобальной системе координат.
| Формулы перевода из локальных координат в глобальные |
|---|
|
X0=XR+X1*cos(AR)-Y1*sin(AR) Y0=YR+Y1*cos(AR)+X1*sin(AR) |
| Формулы обратного перевода координат |
|
X1=(X0-XR)*cos(AR)+(Y0-YR)*sin(AR) Y1=(Y0-YR)*cos(AR)-(X0-XR)*sin(AR) |
Проверим: (переведем координаты туда и обратно)
X1=(X0-XR)*cos(AR)+(Y0-YR)*sin(AR)= =(XR+X1*cos(AR)-Y1*sin(AR)-XR)*cos(AR)+(YR+Y1*cos(AR)+X1*sin(AR)-YR)*sin(AR)= =(X1*cos(AR)-Y1*sin(AR))*cos(AR)+(Y1*cos(AR)+X1*sin(AR))*sin(AR)= =X1*cos(AR)*cos(AR)-Y1*sin(AR)*cos(AR)+Y1*cos(AR)*sin(AR)+X1*sin(AR)*sin(AR)= =X1*cos(AR)*cos(AR)+X1*sin(AR)*sin(AR)=X1*(cos(AR)*cos(AR)+sin(AR)*sin(AR))=X1*(1)=X1,
и вторую координату:
Y1=(Y0-YR)*cos(AR)-(X0-XR)*sin(AR)= =(YR+Y1*cos(AR)+X1*sin(AR)-YR)*cos(AR)-(XR+X1*cos(AR)-Y1*sin(AR)-XR)*sin(AR)= =(Y1*cos(AR)+X1*sin(AR))*cos(AR)-(X1*cos(AR)-Y1*sin(AR))*sin(AR)= =Y1*cos(AR)*cos(AR)+X1*sin(AR)*cos(AR)-X1*cos(AR)*sin(AR)+Y1*sin(AR)*sin(AR)= =Y1*cos(AR)*cos(AR)+Y1*sin(AR)*sin(AR)=Y1*(cos(AR)*cos(AR)+sin(AR)*sin(AR))=Y1*(1)=Y1.
Принадлежность точки отрезку
Это достаточно простая проверка. Пусть точка имеет координаты (x,y), а отрезок (xa,ya)-(xb,yb). Тогда точка принадлежит отрезку, если:
1) выполняется равенство (xb-xa)*(y-ya)=(x-xa)*(yb-ya)
Этим мы проверили, что отрезки (xa,ya)-(xb,yb) и (xa,ya)-(x,y) параллельны или один из них является точкой. Второе условие - точка принадлежит прямой A*x+B*y+C=0, определяемой отрезком (xa,ya)-(xb,yb), либо этот отрезок вырожден в точку:
2) A*x+B*y+C=0, где A=ya-yb, B=xb-xa, C=xa*yb-ya*xb
И наконец точка лежит на этой прямой внутри отрезка:
3) min(xa,xb)<=x<=max(xa,xb) 4) min(ya,yb)<=y<=max(ya,yb)
Всё, теперь все условия проверены.
Пересчение двух отрезков
Часто в робототехнике требуется определить пересекаются ли два отрезка, и если пересекаются, то в какой точке (или по какому отрезку). Например, это нужно для поиска путей на карте (проверяем пересечение пути робота с препятствиями заданными многоугольниками) или для вычисления расстояния до препятсвий (когда ищем точку пересечения луча ИК-дальномера с препятствием, нанесенным на карте и сравниваем с расстоянием, которое нам показывает дальномер).
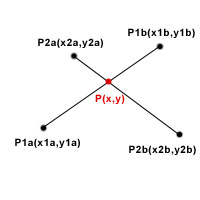
Постановка задачи: Даны два отрезка P1a(x1a,y1a)-P1b(x1b,y1b) и P2a(x2a,y2a)-P2b(x2b,y2b). Требуется определить, пересекаются ли эти два отрезка, если пересекаются, то в какой точке или по какому отрезку.
Решение:
Во-первых определим параллельны ли эти отрезки (если один из отрезков - точка, тогда отрезки считаются параллельными). Для этого проверим выполнение равенства (x1b-x1a)/(y1b-y1a)=(x2b-x2a)/(y2b-y2a), а чтобы не связываться с делением на ноль умножим обе части на (y1b-y1a)*(y2b-y2a), получив (x1b-x1a)*(y2b-y2a)=(x2b-x2a)*(y1b-y1a). Если это равенство выполняется, тогда отрезки параллельны (точного обоснования для случая y1a=y1b или y2a=y2b мы не приводим, вы сами сможете легко убедиться в правильности условия, проверив эти варианты).
Далее решение распадается на 2 варианта:
1. Если отрезки не параллельны, тогда выпишем уравнения прямых на которых лежит каждый отрезок. Общее уравнение первой прямой на плоскости выглядит как A1*x+B1*y+C1=0, если первый отрезок (x1a,y1a)-(x1b,y1b) принадлежит этой прямой, тогда можно принять A1=y1a-y1b, B1=x1b-x1a, C1=x1a*(y1b-y1a)+y1a*(x1a-x1b)=x1a*y1b-y1a*x1b. Аналогично для второй прямой A2*x+B2*y+C2=0 можно принять A2=y2a-y2b, B2=x2b-x2a, C2=x2a*y2b-y2a*x2b. Теперь можно найти точку пересечения этих прямых как решение системы уравнений:
A1*x+B1*y+C1=0, где A1=y1a-y1b, B1=x1b-x1a, C1=x1a*y1b-y1a*x1b, A2*x+B2*y+C2=0, где A2=y2a-y2b, B2=x2b-x2a, C2=x2a*y2b-y2a*x2b.
Легко проверить, что получилось D=A1*B2-A2*B1<>0 (учитывая что отрезки были не параллельны), теперь можно выписывать решение этой системы линейных уравнений:
Выведем из второго уравнения x=(-C2-B2*y)/A2, и подставим в первое: -A1*(C2+B2*y)/A2+B1*y+C1=0, сгруппируем множители y - (B1-A1*B2/A2)*y + (C1-A1*C2/A2)=0, умножим полученное равенство на A2 и перенесем часть с y в другою сторону, получив (A1*B2-A2*B1)*y=(C1*A2-A1*C2), то есть y=(C1*A2-A1*C2)/D.
Выведем
x=(-C2-B2*y)/A2=(-C2-B2*(C1*A2-A1*C2)/D)/A2= =(-C2*D-B2*(C1*A2-A1*C2))/(A2*D)=(-C2*(A1*B2-A2*B1)-B2*(C1*A2-A1*C2))/(A2*D)= =(-C2*A1*B2+C2*A2*B1-B2*C1*A2+B2*A1*C2)/(A2*D)=(C2*A2*B1-B2*C1*A2)/(A2*D)= =(C2*B1-B2*C1)/D.
Не смотря на то, что мы по ходу наших вычислений делили на величины отличные от D, в итоговых формулах все эти деления исчезли и легко проверить, что полученные ответы являются решением системы при D<>0. А это гарантировано тем, что мы проверяли наши отрезки на непараллельность.
Итак, решение системы:
y=(C1*A2-A1*C2)/D x=(C2*B1-B2*C1)/D
Осталось проверить, принадлежит ли это решение обоим отрезкам. Сделать это очень легко:
min(x1a,x1b) <= x <= max(x1a,x1b) min(x2a,x2b) <= x <= max(x2a,x2b) min(y1a,y1b) <= y <= max(y1a,y1b) min(y2a,y2b) <= y <= max(y2a,y2b)
Всё. Если пересечение принадлежит обоим отрезкам, тогда отрезки пересекаются в этой точки, иначе они не пересекаются.
2. Если же отрезки параллельны, тогда проверим, что какой-нибудь из них не является точкой:
Первый отрезок точка, если x1a=x1b и y1a=y1b. Второй отрезок точка, если x2a=x2b и y2a=y2b.
Если один из отрезков является точкой, тогда достаточно проверить принадлежность этой точки другому отрезку:
Точка x,y принадлежит отрезку (x1a,x1b)-(y2a,y2b), если:
min(x1a,x1b) <= x <= max(x1a,x1b) min(y1a,y1b) <= y <= max(y1a,y1b)
Иначе, если оба отрезка не точки и параллельны, тогда надо проверить что отрезки лежат на одной прямой:
A1*x+B1*y+C1=0, где A1=y1a-y1b, B1=x1b-x1a, C1=x1a*y1b-y1a*x1b.
Так как прямые параллельны, то у второй можно принять A2=A1, B2=B1 и только рассчитать C2:
C2=-A1*x2a-B1*y2a.
Если C1<>C2 тогда прямые на которых лежат отрезки не имеют общих точек, а значит отрезки не пересекаются.
Остался случай, когда прямые совпадают. Тогда допустим x1a<>x1b (иначе будем делать то же самое с координатами y)
Отрезки не пересекаются, если:
max(x1a,x1b)<min(x2a,x2b) или min(x1a,x1b)>max(x2a,x2b)
Иначе координаты x отрезка по которому они пересекаются:
(XP1,YP1)-(XP2,YP2) XP1=max(min(x1a,x1b),min(x2a,x2b)) и XP2=min(max(x1a,x1b),max(x2a,x2b)) YP1=-(C1-A1*XP1)/B1 и YP2=-(C1-A1*XP2)/B1
Теперь всё. Все возможные варианты рассмотрены. Понятно, что если на входе гарантировать, что ни один из отрезков не является точкой, то процедура значительно упрощается.