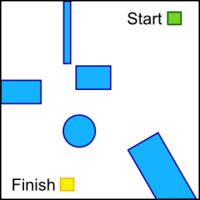
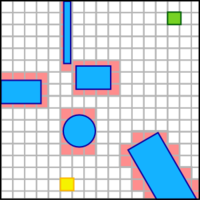
Перемещение робота в нужную точку растровой карты
|
Это незавершённая статья по робототехнике. Вы можете помочь проекту, исправив и дополнив её. |
Постановка классической задачи поиска пути на растровой карте
При решении этой задачи обычно считается, что робот может поворачиваться в нужную сторону вокруг своей оси на месте (танковый поворот). Время, затрачиваемое роботом на поворот, обычно не имеет значения, либо, если требуется найти самый быстрый путь, этим временем пренебрегают или вводят так называемый штраф. Об этом ниже.
Сама постановка классической задачи перемещения робота в нужную точку растровой карты обычно формулируется следующим образом:
Дано: Растровая карта с указанными на ней препятствиями, текущее положение робота и конечное положение, куда нужно попасть.
Требуется: Составить маршрут (последовательность клеток карты), не проходящую через занятые препятствиями клетки и приводящий в нужную точку карты за приемлемое или оптимальное время.
Решение классической задачи поиска пути на карте
Алгоритм А*[1], называемым так же "заливкой" за то, что процесс поиска пути в лабиринте напоминает движение разливающейся по нему жидкости. Этот алгоритм - упрощенный вариант алгоритма Дейкстры, применяющийся для растровых карт. Например, с помощью данного алгоритма просчитывается путь шариков в широко известной игре Lines. Итак, имеем растровое поле 10х10 клеток. Стартовая позиция робота обозначена как "S". Целевая клетка - как "F". Символами "W" обозначены препятствия.
Исходное состояние карты:
| W | |||||||||
| S | W | ||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | |||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | F | ||||||||
| W |
Поскольку у графа для растровой карты все ребра одинаковой длины и веса (в нашем случае пересеченность местности не рассматривается, клетка либо может быть преодолена, либо нет), то учет расстояния от одной вершины до другой ожет быть выражен простым прибавлением единицы. Итак, заполняем карту последовательно увеличивающимися цифрами. Начинаем с точки финиша.
Шаг первый:
|
Шаг второй:
|
Шаг третий:
|
Шаг четвертый:
|
Сделав таким образом N-ое количество шагов, получим следующую картину.
Шаг N-ый:
| 10 | 10 | 10 | 10 | 10 | W | 8 | 8 | 8 | 8 |
| 9 | S | 9 | 9 | 9 | W | 7 | 7 | 7 | 7 |
| 9 | 8 | 8 | 8 | 9 | W | 6 | 6 | 6 | 6 |
| W | W | 7 | W | W | W | 5 | 5 | 5 | 5 |
| 7 | 6 | 6 | W | 4 | 4 | 4 | 4 | 4 | 4 |
| 7 | 6 | 5 | W | 3 | 3 | 3 | 3 | 3 | 4 |
| 7 | 6 | 5 | 4 | 3 | 2 | 2 | 2 | 3 | 4 |
| 7 | 6 | 5 | W | W | W | 1 | W | W | 3 |
| 7 | 6 | 6 | W | 2 | 1 | F | 1 | 2 | 3 |
| 7 | 7 | 7 | W | 2 | 1 | 1 | 1 | 2 | 3 |
На самом деле, заполнение матрицы можно было остановить уже после 8-го шага, т.к. мы достигли точки "S", а значит путь найден. Если весь растр заполнен цифрами, а точка "S" не достигнута, значит пути не существует. Теперь, имея такую заполненную карту, найти путь не сложно - достаточно стартовать из точки "S" и двигаться в соседнюю клетку с наименьшей цифрой. Таким образом найденный путь будет следующим:
| 10 | 10 | 10 | 10 | 10 | W | 8 | 8 | 8 | 8 |
| 9 | S | 9 | 9 | 9 | W | 7 | 7 | 7 | 7 |
| 9 | 8 | 8 | 8 | 9 | W | 6 | 6 | 6 | 6 |
| W | W | 7 | W | W | W | 5 | 5 | 5 | 5 |
| 7 | 6 | 6 | W | 4 | 4 | 4 | 4 | 4 | 4 |
| 7 | 6 | 5 | W | 3 | 3 | 3 | 3 | 3 | 4 |
| 7 | 6 | 5 | 4 | 3 | 2 | 2 | 2 | 3 | 4 |
| 7 | 6 | 5 | W | W | W | 1 | W | W | 3 |
| 7 | 6 | 6 | W | 2 | 1 | F | 1 | 2 | 3 |
| 7 | 7 | 7 | W | 2 | 1 | 1 | 1 | 2 | 3 |
Безусловно, данный алгоритм в представленном виде не отличается интеллектуальностью. Однако он легко модифицируется. В него не трудно добавить учет пересеченности местности или любую другую оценку пройденного пути для выбора оптимального а не кратчайшего маршрута. Подробнее об этом алгоритме можно почитать в статье, посвященной игровым алгоритмам.
