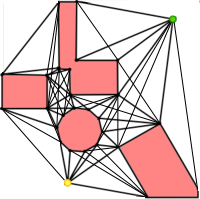
Перемещение робота в нужную точку векторной карты
Содержание
Постановка классической задачи поиска пути на карте
При решении этой задачи обычно считается, что робот может поворачиваться в нужную сторону вокруг своей оси на месте (танковый поворот). Время, затрачиваемое роботом на поворот, обычно не имеет значения, либо, если требуется найти самый быстрый путь, этим временем пренебрегают или вводят так называемый штраф. Об этом ниже. Сама постановка классической задачи перемещения робота в нужную точку карты обычно формулируется следующим образом:
Дано: Карта с указанными на ней препятствиями, текущее положение робота и конечное положение, куда нужно попасть.
Требуется: Составить маршрут (ломаную от текущей точки до нужной), позволяющий избежать всех препятствий и приводящий в нужную точку карты за приемлемое или оптимальное время.
При этом под "положением робота" могут пониматься как "координаты робота", так и пара "координаты робота + направление робота".
Решение классической задачи поиска пути на карте
Переход к задаче поиска пути во взвешенном графе
Наиболее простой подход - составить граф допустимых путей, вершинами которого будут точки карты, а ребрами - доступная возможность проехать из 1 точку в другую напрямую, избежав препятствия.
Дадим некоторые определения: Граф - это совокупность точек (вершин графа) в пространстве и соединяющих их отрезков или связей (ребер графа). В графе могут быть соединены как каждая вершина с каждой (полносвязный граф), так и отдельные вершины друг с другом. Взвешенный граф - это граф, каждое из ребер которого имеет вес (стоимость). Данный тип графа позволяет искать оптимальный маршрут с точки зрения стоимости. Так например, если взвешенный граф описывает пересеченную местность, то вес ребра графа может обозначать степень пересеченности местности (чем больше цифра - тем более пересеченная местность, а значит больше затраты времени на преодоление участка). В этом случае поиск пути с меньшим суммарным весом даст наиболее оптимальный путь с точки зрения затрат времени.
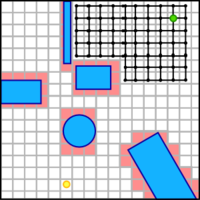
Итак, вернемся к поиску пути во взвешенном графе. В случае растровой карты за вершины графа принимаются центры клеток, а за ребра - возможность проехать в соседние клетки. В случае же векторной карты, понятно, что вообще таких точек на карте бесконечное множество, но мы можем выбрать конечное число точек на карте, чтобы незначительно ограничить свои возможности и уже на этих точках искать оптимальный маршрут. Обязательное условие - в список вершин этого графа должны входить точки старта и финиша (где мы сейчас находимся и куда нам нужно попасть). Когда граф допустимых путей построен поиск пути на карте сводится к задаче поиска пути во взвешенном графе. А для этого есть очень эффективный "алгоритм Дейкстры"[1].
Построение графа допустимых путей для векторной карты
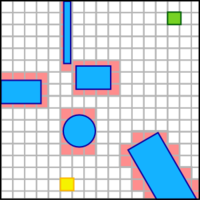
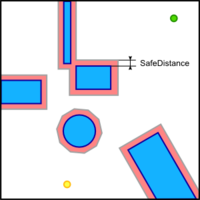
Для построения этого графа мы должны определить некоторое множество вершин, кроме начальной и конечной, находящихся на карте вне препятствий и на некотором расстоянии SafeDistance от них. Это расстояние требуется как минимум для того, чтобы мы могли строить траекторию перемещения центра робота, а про его габариты забыть. Таким образом, минимальное значение SafeDistance - это расстояние от центра робота до самой его выступающей части. Другое определение, которое можно дать величине SafeDistance, - это радиус описанной вокруг робота окружности (полностью в себя его включает) с центром, совпадающим с центром робота. Введение этого параметра позволяет нам выделить на карте группу точек, которые гарантируют, что робот не заденет ни одно из препятствий, если его центр будет принадлежать этой группе. Для выделения такой группы точек необходимо все препятствия обвести границами, отстоящими от них на расстояние не менее SafeDistance.
Простейший способ одновременно выявить все нужные нам вершины и обвести препятствия - создать дополнительную карту, состоящую из многоугольников, являющихся границами препятствий, при этом очевидно мы можем балансировать между точностью границ (а значит потенциально - между возможностью проложить путь по полученной карте) и количеством полученных на выходе вершин (а значит - временем поиска пути и требованиям к памяти).
Сформулируем правила перехода от карты препятствий к карте-основе для построения графа:
- Препятствия, заданные в форме окружностей, приближенно представляем правильными многоугольниками (количество вершин - параметр оптимизации).
- Препятствия, заданные в форме отрезков, обводим прямоугольниками со скругленными с помощью ломаных углами (количество дополнительных вершин для скругления - так же параметр оптимизации).
- Препятствия, представленные в форме ломаных или многоугольников, можно считать набором препятствий в форме отрезков, это чрезвычайно неоптимально с точки зрения вершин, которые потом нужно хранить и обрабатывать при поиске пути, зато очень просто. А можно корректно строить оболочку этих препятствий в форме многоугольника, в котором приближения скруглений на границах выпуклых углов будут представленными ломанными, количество точек в которых так же является параметром оптимизации.
- Не забываем, что граница препятствия создается на расстоянии SafeDistance от самого препятствия.
После построения такой карты границ препятствий можно легко составить граф допустимых путей на базе вершин многоугольников из только что построенной карты и начальной + конечной вершин. При этом, конечно, каждое ребро графа допустимо, если не пересекает какой-либо границы препятствия.
Решение задачи поиска пути во взвешенном графе алгоритмом Дейкстры
Для удобства расстоянием D[i] от стартовой вершины до любой другой вершины i будем называть длину минимального пути от стартовой вершины до вершины i. Суть алгоритма сводится к тому, что все вершины i, в которые можем попасть из стартовой, мы обрабатываем в порядке возрастания D[i]. Понятно, что с самого начала у нас нет информации обо всех D[i], но у нас точно есть информация о минимальном D[i]=0 - это когда i - стартовая вершина. Поэтому мы можем спокойно обрабатывать её. В процессе её обработки мы перебираем все вершины в которые можно из неё попасть и смотрим какая ближайшая. Очевидно, что это будет следующий по порядку D[i], а значит мы нашли следующую вершину которую можно обрабатывать под номером 2. И так далее.
Полностью алгоритм Дейкстры будет приведен ниже. Здесь же проиллюстрируем этот алгоритм простейшим примером - алгоритмом А*, называемым так же "алгоритм воды" за то, что процесс поиска пути в лабиринте напоминает движение разливающейся по нему жидкости. Этот алгоритм - упрощенный вариант алгоритма Дейкстры, применяющийся для растровых карт. Например, с помощью данного алгоритма просчитывается путь шариков в широко известной игре Lines. Итак, имеем растровое поле 10х10 клеток. Стартовая позиция робота обозначена как "S". Целевая клетка - как "F". Символами "W" обозначены препятствия.
Исходное состояние карты:
| W | |||||||||
| S | W | ||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | |||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | F | ||||||||
| W |
Поскольку у графа для растровой карты все ребря одинаковой длины и в нашем случае веса (пересеченность местности не рассматривается, клетка либо может быть преодолена, либо нет), то учет расстояния от одной вершины до другой ожет быть выражен простым прибавлением единицы. Итак, заполняем карту последовательно увеличивающимися цифрами. Начинаем с точки финиша. Шаг первый:
| W | |||||||||
| S | W | ||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | |||||||||
| W | |||||||||
| W | W | W | 1 | W | W | ||||
| W | 1 | F | 1 | ||||||
| W | 1 | 1 | 1 |
Шаг второй:
| W | |||||||||
| S | W | ||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | |||||||||
| W | |||||||||
| 2 | 2 | 2 | |||||||
| W | W | W | 1 | W | W | ||||
| W | 2 | 1 | F | 1 | 2 | ||||
| W | 2 | 1 | 1 | 1 | 2 |
Шаг третий:
| W | |||||||||
| S | W | ||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | |||||||||
| W | 3 | 3 | 3 | 3 | 3 | ||||
| 3 | 2 | 2 | 2 | 3 | |||||
| W | W | W | 1 | W | W | ||||
| W | 2 | 1 | F | 1 | 2 | 3 | |||
| W | 2 | 1 | 1 | 1 | 2 | 3 |
Шаг четвертый:
| W | |||||||||
| S | W | ||||||||
| W | |||||||||
| W | W | W | W | W | |||||
| W | 4 | 4 | 4 | 4 | 4 | 4 | |||
| W | 3 | 3 | 3 | 3 | 3 | 4 | |||
| 4 | 3 | 2 | 2 | 2 | 3 | 4 | |||
| W | W | W | 1 | W | W | ||||
| W | 2 | 1 | F | 1 | 2 | 3 | |||
| W | 2 | 1 | 1 | 1 | 2 | 3 |
Сделав таким образом N-ое количество шагов, получим следующую картину. Шаг N-ый:
| 10 | 10 | 10 | 10 | 10 | W | 8 | 8 | 8 | 8 |
| 9 | S | 9 | 9 | 9 | W | 7 | 7 | 7 | 7 |
| 9 | 8 | 8 | 8 | 9 | W | 6 | 6 | 6 | 6 |
| W | W | 7 | W | W | W | 5 | 5 | 5 | 5 |
| 7 | 6 | 6 | W | 4 | 4 | 4 | 4 | 4 | 4 |
| 7 | 6 | 5 | W | 3 | 3 | 3 | 3 | 3 | 4 |
| 7 | 6 | 5 | 4 | 3 | 2 | 2 | 2 | 3 | 4 |
| 7 | 6 | 5 | W | W | W | 1 | W | W | |
| 7 | 6 | 6 | W | 2 | 1 | F | 1 | 2 | 3 |
| 7 | 7 | 7 | W | 2 | 1 | 1 | 1 | 2 | 3 |
На самом деле, заполнение матрицы можно было остановить уже после 8-го шага, т.к. мы достигли точки "S", а значит путь найден. Если весь растр заполнен цыфрами, а точка "S" не достигнута, значит пути не существует. Теперь, имея такую заполненную карту, найти путь не сложно - достаточно стартовать из точки "S" и двигаться в соседнюю клетку с наименьшей цифрой. Таким образом найденный путь будет следующим:
| 10 | 10 | 10 | 10 | 10 | W | 8 | 8 | 8 | 8 |
| 9 | S | 9 | 9 | 9 | W | 7 | 7 | 7 | 7 |
| 9 | 8 | 8 | 8 | 9 | W | 6 | 6 | 6 | 6 |
| W | W | 7 | W | W | W | 5 | 5 | 5 | 5 |
| 7 | 6 | 6 | W | 4 | 4 | 4 | 4 | 4 | 4 |
| 7 | 6 | 5 | W | 3 | 3 | 3 | 3 | 3 | 4 |
| 7 | 6 | 5 | 4 | 3 | 2 | 2 | 2 | 3 | 4 |
| 7 | 6 | 5 | W | W | W | 1 | W | W | |
| 7 | 6 | 6 | W | 2 | 1 | F | 1 | 2 | 3 |
| 7 | 7 | 7 | W | 2 | 1 | 1 | 1 | 2 | 3 |
Безусловно, данный алгоритм в представленном виде не отличается интеллектуальностью. Однако он легко модифицируется. В него не трудно добавить учет пересеченности местности или любую другую оценку пройденного пути для выбора оптимального а не кратчайшего маршрута.
| Входные данные и используемые функции: |
|---|
|
Инициализация алгоритма заключается в пометке всех вершин как необработанных (Flag[i]=0), указании для всех вершин длины пути +бесконечность (D[start]=max_len), кроме стартовой (для неё указываем D[start]=0) и помещении стартовой вершины start в очередь Q.
Для всех вершин v из V выполняем:
Flag[v]=0
D[v]=+бесконечность
D[start]=0
Q={start}
Итерации основного цикла алгоритма повторяются до тех пор, пока множество Q не пусто. На каждом шаге мы извлекаем вершину i из множества Q, путь до которой D[i] минимален и обрабатываем её следующим образом: для всех еще не обработанных вершин, в которые мы можем попасть из неё делаем 2 операции:
- Если этой вершины еще нет в множестве Q, тогда добавляем её в это множество;
- Если D[i]+Len(i,j)<D[j], тогда запоминаем более короткий путь D[j]=D[i]+Len(i,j);
Пока Q не пусто выполняем:
i=ExtractMin(Q)
Flag[i]=1
Для всех v из adj(i) выполняем:
Если Flag[v]=0 тогда Q={Q,v}
Если D[v]<D[i]+len(i,v) тогда D[v]=D[i]+len(i,v)
По окончании основного цикла для всех вершинах, в которые мы можем попасть из стартовой в D[i] будет храниться +бесконечность, если в эту вершину нельзя пройти, либо минимальная длина пути, если в эту вершину пройти можно.
Чтобы извлечь теперь оптимальный маршрут из полученного массива оптимальных расстояний нам потребуется выполнить обратный пробег по ребрам из вершины путь куда требуется найти до стартовой вершины.
Для этого достаточно завести массив для сохранения в нем найденного пути, положив там первым элементом целевую вершину, положить в рабочую переменную i целевую вершину finish и пока в рабочей переменной не окажется стартовой вершины выполнять цикл, в котором находить вершину j из которой мы могли оптимальным путем прийти в текущую вершину i (D[i]=D[j]+Len(i,j)) и присваивать её текущей вершине (i=j) и добавлять найденную вершину в массив найденного пути. Тогда при завершении работы этого цикла в массиве окажется найденный оптимальный путь, только выписанный задом наперед (первая вершина - finish, последняя - start).
W={finish}
i=finish
Пока i не равно start выполняем:
j=i
Для всех v из adj(i) пока j равно i выполняем:
Если D[i]=D[v]+len(v,i) тогда j=i
W={W,j}
i=j
Проблемы поиска оптимального пути по карте в реальности и способы их решения
В реальности существует масса различных факторов, которые не были учтены в рассматренной выше ситуации. Мы попробуем разобрать основные проблемы и указать возможные способы их решения:
Учет погрешности выполнения команд на перемещение роботом
Понятно, что это только в программе мы можем с нужной нам точностью посчитать столкновение робота с препятствием, а в реальности существуют погрешности исполнительных устройств, приводящие к отклонениям от запланированной траектории. Поэтому имеет смысл на карте провести границу вокруг всех препятствий на таком расстоянии SafeDistance, что вероятность отклонения шасси робота от запланированной траектории на большую чем SafeDistance величину не будет превышать допустимую. Разумеется при этом не стоит избегать использования систем защиты от столкновения, имеющих приоритеты над модулем навигации и не допускающих незапланированного столкновения робота с предметами окружения.
Учет времени, затрачиваемого на повороты на месте
В указанном выше алгоритме очевидным упущением является то, что не учитывается время, затрачиваемое на остановку, развороты робота в вершинах графа и разгон, требующиеся для движения в следующих направлениях. Здесь можно применить очень простой подход - ввести штраф за "возможно остановку и возможно требующийся поворот" в каждой промежуточной вершине, в этом случае просто все формулы вида D[j]=D[i]+Len(i,j) заменяться на D[j]=D[i]+Len(i,j)+СуммаШтрафа.
Понятно что при этом не учитывается сколько времени робот будет поворачиваться (на какой угол требуется поворот), но и это можно учесть предельно точно, сильно пожертвовав производительностью и объемом памяти требующимся для вычислений. Для этого достаточно "размножить" каждую вершину, начав считать "вершиной графа" пару "вершина и по какому ребру мы в неё пришли". Тогда СуммуШтрафа можно посчитать точно разложив её на составляющую штрафа за торможение и разгон и составляющую штрафа на поворот с направления X (откуда пришли в вершину) до направления Y (в какое ребро сейчас будем двигаться. Так же ясно, что этот подход позволяет учесть начальную ориентацию робота и конечную ориентацию, если её требуется достичь.
Оптимизация маршрута путем избегания поворотов "на месте"
Понятно, что если мы сможем проходить маршрут не останавливаясь на каждом повороте, то мы сможем делать это значительно быстрее. Один из наиболее простых вариантов - попробовать увеличить дистанцию безопасности SafeDistance, чтобы можно было повороты под небольшим углом проводить не снижая скорость до нулевой и заменяя участки движения "тормозим, поворачиваем, разгоняемся" на "чуть снижаем скорость, входим в поворот в движении, разгоняемся по следующему направлению". Основная проблема здесь - при значительном увеличении SafeDistance на карте может вообще не оказаться путей к целевой точке, либо они окажутся неоптимальными, потому что будет существовать более короткий маршрут, но со значительным снижением скорости. Имеет смысл попробовать перебрать несколько значений SafeDistance (от требующего повороты на месте до требующего малых снижений скоростей на поворотах) и сравнить найденные маршруты по общему времени прохождения. Кроме того можно пробовать комбинировать получившиеся при разных SafeDistance маршруты или применять более сложные смешанные алгоритмы.
Поиск маршрута для робота, неспособного поворачиваться на месте
Здесь будет рассмотрены проблемы поиска маршрута для роботов не имеющих возможности развернуться на месте (например, любой обычный автомобиль не имеет такой возможности).
Примечания
- ↑
Эдсгер Вибе Дейкстра (Edsger Wybe Dijkstra; 11 мая 1930 — 6 августа 2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.
Об Э.В.Дейкстре в Википедии
Об алгоритме Дейкстры в Википедии