Генетические алгоритмы в МиниБоте — различия между версиями
EdGull (обсуждение | вклад) |
EdGull (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| + | |||
== '''Генетические алгоритмы: почему они работают? когда их применять?''' == | == '''Генетические алгоритмы: почему они работают? когда их применять?''' == | ||
| − | |||
'''РОСС КЛЕМЕНТ, Опубликовано: 16.3.1999''' | '''РОСС КЛЕМЕНТ, Опубликовано: 16.3.1999''' | ||
| Строка 85: | Строка 85: | ||
Реализация генетического алгоритма предполагает задание функции приспособленности, или фитнес-функции (fitness function). Эта функция получает на вход двоичную хромосому и возвращает число, показывающее, насколько хороша эта хромосома. В реализованном автором генетическом алгоритме решения ЗКВ сначала определяется наихудшая хромосома (отвечающая самому длинному из маршрутов) и измеряется длина этого маршрута (в километрах). Полученное число умножается на 1,1 и объявляется плохой длиной, по отношению к которой оценивается качество остальных хромосом: приспособленность хромосомы вычисляется как разность между плохой длиной и длиной маршрута, заданного данной хромосомой. В результате этих несколько запутанных вычислений каждой хромосоме ставится в соответствие ее приспособленность (fitness) - число, которое оказывается сравнительно маленьким для плохих (длинных) маршрутов и сравнительно большим для хороших (коротких) маршрутов. | Реализация генетического алгоритма предполагает задание функции приспособленности, или фитнес-функции (fitness function). Эта функция получает на вход двоичную хромосому и возвращает число, показывающее, насколько хороша эта хромосома. В реализованном автором генетическом алгоритме решения ЗКВ сначала определяется наихудшая хромосома (отвечающая самому длинному из маршрутов) и измеряется длина этого маршрута (в километрах). Полученное число умножается на 1,1 и объявляется плохой длиной, по отношению к которой оценивается качество остальных хромосом: приспособленность хромосомы вычисляется как разность между плохой длиной и длиной маршрута, заданного данной хромосомой. В результате этих несколько запутанных вычислений каждой хромосоме ставится в соответствие ее приспособленность (fitness) - число, которое оказывается сравнительно маленьким для плохих (длинных) маршрутов и сравнительно большим для хороших (коротких) маршрутов. | ||
| + | |||
| + | '''Рис. 3. Декодирование двоичной хромосомы.''' [[Изображение:20-3.gif|thumb]] | ||
| + | '''Рис. 4. Выбор при помощи колеса рулетки.''' [[Изображение:20-4.gif|thumb]] | ||
| + | |||
| + | Вернемся к "выживанию сильнейших". Будем использовать "колесо рулетки" для того, чтобы выбрать из текущего поколения хромосомы, которые сохранятся в следующем поколении. Если читатель представляет себе обычную рулетку, он согласится, что у шарика одинаковые шансы остановиться в любом из секторов. Но если рулетка разделена на неравные секторы (рис. 4), вероятность того, что шарик остановится в широком секторе, велика, а в узком - мала. Предположим, что каждый сектор нашей "кривой" рулетки отвечает одной из хромосом, а ширина сектора пропорциональна ее качеству. Запустив рулетку 500 раз, мы получим новое поколение хромосом. | ||
| + | |||
| + | Так как рулетка "кривая", вполне возможно, что некоторые из хромосом данного поколения будут выбраны несколько раз, а некоторые - ни разу. Хотя случайный характер выбора и может привести к отсеву ("смерти") очень хорошо приспособленных хромосом и увеличению количества плохо приспособленных хромосом, в среднем число хороших хромосом будет расти, а плохих - уменьшаться. Можно ожидать, что качество следующей популяции будет, в среднем, выше качества предыдущей. Начинают работать факторы эволюции, так как хромосомы фактически вынуждены бороться за место в следующем поколении под действием "искусственного дефицита" (artificial scarcity). | ||
| + | |||
| + | Однако здесь возникает вопрос: получили ли мы лучшие решения, чем те, что были в предыдущем поколении? Короткий ответ: нет, не получили. Колесо рулетки не создает новых решений. Первое, что нужно для создания таких решений, - кроссинговер (crossover). | ||
Версия 18:42, 19 июля 2008
Генетические алгоритмы: почему они работают? когда их применять?
РОСС КЛЕМЕНТ, Опубликовано: 16.3.1999
взято от сюда http://www.mnogosmenka.ru/drugoe/genetitiskie.htm
© 2002, Издательский дом «КОМПЬЮТЕРРА» | http://www.computerra.ru/
Журнал «Компьютерра» | http://www.computerra.ru/
Этот материал Вы всегда сможете найти по его постоянному адресу: http://www.computerra.ru/offline/1999/289/2523/
XIX веке Чарльз Дарвин совершил кругосветное плавание, собирая информацию для теории эволюции на основе естественного отбора, при котором выживает сильнейший. Мог ли он предполагать, что сто лет спустя математики будут использовать эту теорию для решения задачи об оптимальном маршруте кругосветного путешествия с остановками на многих маленьких островах?..
Росс Клемент (Ross Clement; R.P.Clement@westminster.ac.uk) окончил Оклендский университет (Новая Зеландия) по специальности "Компьютерные науки". Защитил диссертацию и получил степень "Doctor of Engineering" в Техническом университете Тойохаши (Toyohashi University of Technology) в Японии. В 1991-93 годах занимался приложениями генетических алгоритмов к задачам составления расписаний. С 1993 года - лектор в Школе компьютерных наук в Харроу, в Университете Вестминстера (Лондон). Научные интересы: генетические алгоритмы, интеллектуальные агенты, фрактальная музыка.
Рис. 1.Эффективный и неэффективный маршруты в задаче коммивояжера (ЗКВ).
Круг практических задач, решаемых компьютерами, постоянно расширяется. Компьютер может составить расписание деловых встреч, удобный график работы сменных экипажей автобусов, научить вас играть на пианино, а иногда и заставить задуматься, способны ли вы вообще научиться игре в шахматы. Однако это возможно лишь при одном маленьком, но неприятном условии: какой-то несчастный должен написать программу, которая будет все это делать. Как жаль, что мы не можем просто перечислить, что хотелось бы получить от программы, а все скучные детали того, как именно она это сделает, предоставить самой машине! Генетические алгоритмы, конечно, не претендуют на роль эдакого "святого Грааля" в сфере программирования, но в ряде приложений они способны на нечто довольно близкое.
Давайте для примера посмотрим, как можно использовать генетические алгоритмы для решения "задачи коммивояжера" (ЗКВ). ЗКВ состоит в том, чтобы по данному списку городов определить, в каком порядке коммивояжер должен посетить каждый из них по одному разу, чтобы получившийся маршрут был кратчайшим из возможных или хотя бы близким к таковому. На рис. 1 показаны два маршрута для одной задачи ЗКВ - эффективный и менее эффективный (то есть более длинный).
Генетические алгоритмы решают задачи, работая с популяцией из некоторого числа наугад взятых решений (обычно их несколько сотен; далее для определенности примем величину 500). При этом должны быть указаны правила, по которым решения, по аналогии с дарвинской "борьбой за существование":
- скрещиваются (crossover; в русской биологической литературе эта операция традиционно называется кроссинговер),
- порождают разнообразных "детей",
- соперничают за ограниченные ресурсы,
- мутируют
- и, в конечном счете, умирают.
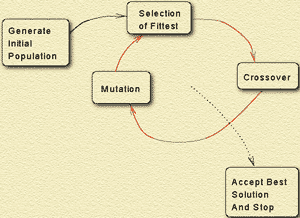
Рис. 2. Схема работы генетического алгоритма.
Схема типичного генетического алгоритма представлена на рис. 2. В статье мы обсудим, как работают различные блоки из этой схемы.
Разработка генетического алгоритма начинается с конструирования двоичной хромосомы, представляющей возможные решения этой задачи. Традиционно генетические алгоритмы используют для этого двоичные строки фиксированной длины. Например, для нашей ЗКВ с четырьмя городами, которые надо поочередно посетить, проще всего было бы выделить по 2 бита на каждый город, получив 8-битовую хромосому. Рисунок 3 поясняет, как записывается информация на такую хромосому. Можно построить множество случайных строк из 8 бит, интерпретируя их как маршруты объезда городов.
Табл. 1. Случайно выбранные хромосомы.
| Chromosome | Meaning |
|---|---|
| 00110010 | Auckland Wellington Auckland Napier |
| 10101100 | Napier Napier Wellington Auckland |
| 10100101 | Napier Napier New Plymouth New Plymouth |
| 01010101 | New Plymouth New Plymouth New Plymouth New Plymouth |
Но эта хромосома слишком проста для ЗКВ любого размера. Один из ее недостатков заключается в том, что большинство двоичных строк из 8 бит не соответствуют допустимым маршрутам. Как видно из таблицы 1, мы можем получить маршруты, проходящие через некоторые города дважды, а через другие - ни разу. Можно было бы рассматривать и такие "не-решения", с тем чтобы настоящие решения вытеснили их в процессе эволюции, но в дальнейшем мы увидим, что это неэффективный путь. Лучше придумать другую кодировку, чтобы любая двоичная строка представляла допустимый (но, конечно, не всегда разумный) маршрут в ЗКВ.
Табл. 1. Случайно выбранные 5-битовые хромосомы.
| Chromosome | Meaning |
|---|---|
| 10111 | Napier Auckland New Plymouth Wellington |
| 00110 | Auckland New Plymouth Napier Wellington |
| 10101 | Auckland New Plymouth Napier Wellingt |
| 01011 | New Plymouth Napier Wellington Auckland |
Вот одна из таких кодировок: первые два бита - номер первого города в маршруте, вторые два бита - номер того из оставшихся трех городов, который посещается вторым, пятый бит определяет выбор из оставшихся двух городов, а на номер последнего, четвертого города битов выделять не нужно. Мы получаем 5-битовую хромосому. В таблице 2 показаны несколько таких хромосом и соответствующих им маршрутов. Заметим, что и здесь возникает небольшая проблема, так как вторые два бита могут представлять четыре различных числа, которые надо сопоставить трем различным городам. С этим можно справиться, решив, что и 11, и 00 соответствуют первому из этих трех городов. Не очень удачное решение, так как оно вдвое повышает шансы наугад выбрать именно этот город, но пока это нам не очень мешает.
Сконструировав хромосому, мы без всякого труда можем построить 500 случайно выбранных маршрутов в нашей ЗКВ, сгенерировав 500 случайных 5-битовых чисел. Но ведь мы как раз и мечтали свести программирование к минимуму при решении трудных задач. Значит, цель достигнута? Разумеется, это зависит от того, насколько хороши полученные таким путем решения. Другими словами, затратит ли наш коммивояжер минимально возможное время на свои переезды из города в город, если воспользуется некоторыми из предлагаемых маршрутов?
В нашем случае ответ, скорее всего, будет утвердительным. 5 бит могут представлять лишь 32 различных числа, поэтому среди нескольких сот случайных маршрутов, наверное, будет и оптимальный. Пространство поиска возможных решений очень мало. К сожалению, трудные для современных компьютеров ЗКВ относятся к нескольким сотням объектов: например, городов или скважин, которые необходимо пробурить, и т. д. В этом случае объем пространства поиска приближается по порядку величины к числу атомов в известной части вселенной, и, по всей вероятности, даже лучшее из пятисот выбранных наугад решений окажется очень плохим. Вот здесь и начинает работать эволюция.
Нам нужно каким-то образом сымитировать "выживание сильнейших" (survival of the fittest), позволяя лучшим хромосомам жить, а не самых лучших обрекая на гибель. Традиция разработки генетических алгоритмов предписывает выбирать каждое последующее поколение (то есть совокупность определенного количества хромосом) путем стохастической, но целенаправленной селекции. Для этого мы должны знать, как отличить хорошие хромосомы от плохих.
Реализация генетического алгоритма предполагает задание функции приспособленности, или фитнес-функции (fitness function). Эта функция получает на вход двоичную хромосому и возвращает число, показывающее, насколько хороша эта хромосома. В реализованном автором генетическом алгоритме решения ЗКВ сначала определяется наихудшая хромосома (отвечающая самому длинному из маршрутов) и измеряется длина этого маршрута (в километрах). Полученное число умножается на 1,1 и объявляется плохой длиной, по отношению к которой оценивается качество остальных хромосом: приспособленность хромосомы вычисляется как разность между плохой длиной и длиной маршрута, заданного данной хромосомой. В результате этих несколько запутанных вычислений каждой хромосоме ставится в соответствие ее приспособленность (fitness) - число, которое оказывается сравнительно маленьким для плохих (длинных) маршрутов и сравнительно большим для хороших (коротких) маршрутов.
Рис. 3. Декодирование двоичной хромосомы.
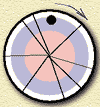
Рис. 4. Выбор при помощи колеса рулетки.
Вернемся к "выживанию сильнейших". Будем использовать "колесо рулетки" для того, чтобы выбрать из текущего поколения хромосомы, которые сохранятся в следующем поколении. Если читатель представляет себе обычную рулетку, он согласится, что у шарика одинаковые шансы остановиться в любом из секторов. Но если рулетка разделена на неравные секторы (рис. 4), вероятность того, что шарик остановится в широком секторе, велика, а в узком - мала. Предположим, что каждый сектор нашей "кривой" рулетки отвечает одной из хромосом, а ширина сектора пропорциональна ее качеству. Запустив рулетку 500 раз, мы получим новое поколение хромосом.
Так как рулетка "кривая", вполне возможно, что некоторые из хромосом данного поколения будут выбраны несколько раз, а некоторые - ни разу. Хотя случайный характер выбора и может привести к отсеву ("смерти") очень хорошо приспособленных хромосом и увеличению количества плохо приспособленных хромосом, в среднем число хороших хромосом будет расти, а плохих - уменьшаться. Можно ожидать, что качество следующей популяции будет, в среднем, выше качества предыдущей. Начинают работать факторы эволюции, так как хромосомы фактически вынуждены бороться за место в следующем поколении под действием "искусственного дефицита" (artificial scarcity).
Однако здесь возникает вопрос: получили ли мы лучшие решения, чем те, что были в предыдущем поколении? Короткий ответ: нет, не получили. Колесо рулетки не создает новых решений. Первое, что нужно для создания таких решений, - кроссинговер (crossover).