Фильтр Калмана — различия между версиями
=DeaD= (обсуждение | вклад) (Новая страница: «The '''Kalman filter''' is an efficient recursive filter that estimates the state of a linear dynamic system...») |
Etopis (обсуждение | вклад) |
||
| (не показаны 72 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | <center><big>(перевод статьи "Kalman Filter" из англоязычной википедии)</big></center> | |
| − | + | <center>Исходная статья: [[w:en:Kalman filter]]</center> | |
| − | + | <p align=center><b>Авторство исходной статьи коллективное</b><br><br><i>Перевод: © Ботов Антон aka =DeaD=, 2009<br><br>Эксклюзивно для www.roboforum.ru<br> копирование на другие ресурсы и публикация перевода<br>без разрешения его автора запрещены</i></p> | |
| − | |||
| − | |||
| − | + | '''Фильтр Калмана''' это эффективный рекурсивный фильтр, который оценивает состояние линейной динамической системы по серии неточных измерений. Он используется в широком спектре задач от радаров до систем технического зрения, и является важной частью теории управления системами. | |
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| − | |||
| − | + | == Примеры решаемых фильтром задач == | |
| − | + | В качестве примера можно привести предоставление точной, поддерживаемой в актуальном состоянии, информации о положении и скорости объекта, при наличии серии измерений положения объекта, каждое из которых в некоторой степени неточно. Например, в радарах при отслеживании цели мы имеем очень зашумлённую (неточную) информацию о положении, скорости и ускорении наблюдаемого объекта. Фильтр Калмана использует известную нам математическую модель динамики объекта, которая описывает какие вообще изменения состояния объекта возможны, чтобы устранить погрешности измерения и предоставить хорошей точности положение объекта в данный момент (фильтрация), в будущие моменты (предсказание), или в какие-то из прошедших моментов (интерполяция или сглаживание). <!-- Not a good place for mentioning the alpha beta filter because the reader doesn't yet even know what the Kalman filter is.--> | |
| − | + | В качестве альтернативного примера рассмотрим старый тихоходный автомобиль, про который точно известно, что он разгоняется от 0 до 100км/ч не менее чем за 10 секунд. Представим, что спидометр этого автомобиля барахлит и показывает скорость с погрешностью 60км/ч от настоящей. Из неподвижного положения, которое измерено точно, потому что колёса не вращались, водитель нажимает педаль газа в пол и через 5 секунд спидометр показывает 110км/ч, но водитель то знает, что машина не может так быстро разогнаться, поэтому он использует информацию о погрешности и понимает, что сейчас скорее всего, учитывая то, что он знает на сколько может врать спидометр, скорость около 50км/ч. Так же и фильтр Калмана использует информацию о погрешности измерений и о том, каким правилам подчиняется динамическая система, для минимизации погрешности измерений и предоставления максимально точной информации о состоянии системы. | |
| − | + | Наглядные примеры в сети: | |
| − | * | + | * [[http://roboforum.ru/viewtopic.php?p=114926#p114926 Применение фильтра калмана для определения линии горизонта]] |
| − | |||
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| + | |||
| + | |||
| + | ==Используемая модель динамической системы== | ||
| + | |||
| + | Фильтры Калмана основываются на линейных динамических системах, дискретизированных по времени. Они моделируются [[:ru:Цепь Маркова|цепями Маркова]], построенными на [[:ru:Линейное отображение|линейных операторах]] с внесенными погрешностями с [[:ru:Нормальное распределение|нормальным Гауссовым распределением]]. Состояние системы считается вектор из действительных чисел. При каждом шаге по времени, линейный оператор применяется к вектору состояния системы, добавляется некоторая погрешность и опционально некоторая информация об управляющих воздействиях на систему, если таковая известна. После чего другим линейным оператором с другой погрешностью добавляется видимая информация о состоянии системы. Фильтр Калмана можно рассматривать в качестве аналога скрытым моделям Маркова, с тем ключевым отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут работать с произвольными распределениями для следующих значений переменных состояния системы, в отличие от модели стандартного Гауссового распределения, поддерживаемого фильтрами Калмана. Существует строгая взаимосвязь между уравнениями фильтра Калмана и аналогичными в скрытых моделях Маркова. Подробней эта тема, как и некоторые другие модели, рассмотрена авторами Roweis и Ghahramani (1999).<ref>Roweis, S. and Ghahramani, Z., ''[http://www.mitpressjournals.org/doi/abs/10.1162/089976699300016674 A unifying review of linear Gaussian models]'', Neural Comput. Vol. 11, No. 2, (February 1999), pp. 305-345. </ref> | ||
| + | |||
| + | Чтобы было возможным использовать фильтр Калмана для оценки внутреннего состояния системы по серии неточных измерений, необходимо представить модель данного процесса в соответствии с универсальной моделью процесс для фильтра Калмана. Это означает, что нужно указать матрицы '''F'''<sub>''k''</sub>, '''H'''<sub>''k''</sub>, '''Q'''<sub>''k''</sub>, '''R'''<sub>''k''</sub>, и иногда '''B'''<sub>''k''</sub> для каждого шага по времени ''k'', как указано ниже. | ||
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| + | |||
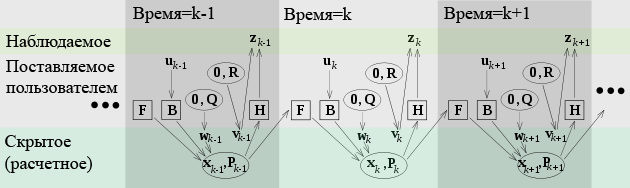
| + | [[Image:Kalman filter model.png|right|thumb|631px|Модель системы, лежащая в основе фильтра Калмана. Квадратиками обозначены матрицы. Эллипсами обозначены нормальные распределения (с указанными в скобках матрицами матожиданий и ковариантностей). Значения без кружочка и квадратика вокруг являются векторами.]] | ||
| + | |||
| + | Модель системы для фильтра Калмана подразумевает, что реальное состояние в момент времени ''k'' получается из состояния в момент времени (''k'' − 1) по правилу: | ||
| + | |||
| + | <math> \textbf{x}_{k} = \textbf{F}_{k} \textbf{x}_{k-1} + \textbf{B}_{k} \textbf{u}_{k} + \textbf{w}_{k} </math>, | ||
| + | |||
| + | где | ||
| + | |||
| + | *'''F'''<sub>''k''</sub> матрица соответствующая модели преобразованию системы со временем, применяемая к предыдущему состоянию '''x'''<sub>''k''−1</sub>; | ||
| + | * '''B'''<sub>''k''</sub> матрица соответствующая модели применения управляющего воздействия, которая применяется к состоянию системы умноженная на вектор управляющего воздействия '''u'''<sub>''k''</sub>; | ||
| + | * '''w'''<sub>''k''</sub> вектор погрешности, которая предполагается, имеет нулевое матожидание, нормальное Гауссово распределение и матрицу [[:ru:Ковариация|ковариаций]] '''Q'''<sub>''k''</sub>: | ||
| + | |||
| + | <math>\textbf{w}_{k} \sim N(0, \textbf{Q}_k) </math> | ||
| + | |||
| + | В момент времени ''k'' производится наблюдение (или измерение) '''z'''<sub>''k''</sub> реального состояния системы '''x'''<sub>''k''</sub> в соответствии с моделью измерения | ||
:<math>\textbf{z}_{k} = \textbf{H}_{k} \textbf{x}_{k} + \textbf{v}_{k}</math> | :<math>\textbf{z}_{k} = \textbf{H}_{k} \textbf{x}_{k} + \textbf{v}_{k}</math> | ||
| − | + | где '''H'''<sub>''k''</sub> матрица, соответствующая модели наблюдения, которая отображает пространство векторов реального состояния системы в пространство векторов результатов наблюдений, а '''v'''<sub>''k''</sub> это вектор ошибки наблюдения, который считается имеющим нулевое матожидание, нормальное Гауссово распределение и матрицу ковариаций '''R'''<sub>''k''</sub>: | |
| + | |||
| + | <math>\textbf{v}_{k} \sim N(0, \textbf{R}_k) </math> | ||
| − | + | Вектор начального состояния системы и векторы погрешностей на каждом шаге {'''x'''<sub>0</sub>, '''w'''<sub>1</sub>, ..., '''w'''<sub>''k''</sub>, '''v'''<sub>1</sub> ... '''v'''<sub>''k''</sub>} считаются не зависящими друг от друга. | |
| − | + | Множество реальных динамических систем не полностью вписываются в эту модель, однако по причине того, что фильтр Калмана предназначен для работы в ситуации неточных данных, ответы, генерируемые этим фильтром, часто являются очень хорошим приближением к правильному ответу, что делает фильтр очень полезным даже в таких ситуациях. Вариации Калмановской фильтрации описанные ниже позволяют работать с более сложными моделями. | |
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| − | |||
| − | |||
| − | + | ==Фильтр Калмана== | |
| − | + | Фильтр Калмана является разновидностью рекурсивного фильтра. Это означает, что только результат предыдущей итерации фильтра (в виде оценки состояния системы и оценки погрешности определения этого состояния) и текущие наблюдения нужны для расчета текущего состояния системы. В отличие от пакетных фильтров не требуется хранение никакой истории наблюдений. В следующем дальше тексте запись <math>\hat{\textbf{x}}_{n|m}</math> означает оценку состояния системы <math>\textbf{x}</math> в момент времени ''n'' при учете наблюдений (измерений) с начала работы фильтра и по момент времени ''m'' включительно. | |
| − | + | Состояние фильтра содержится в двух переменных: | |
| − | === | + | *<math>\hat{\textbf{x}}_{k|k}</math>, оценочное состояние системы в момент времени ''k'', которое получено на основании начального состояния системы и всех наблюдений по момент времени ''k'' включительно; |
| + | *<math>\textbf{P}_{k|k}</math>, матрица ковариаций этого состояния, включающая в себя оценку дисперсий погрешности вычисленного состояния и уровни ковариаций, показывающих выявленные взаимосвязи между параметрами состояния системы. | ||
| + | |||
| + | Итерация фильтра Калмана делится на две фазы: '''Предсказание''' и '''Учет наблюдений'''. Фаза предсказания использует вычисленное на предыдущем шаге состояние для получения через модель системы оценочного состояния на текущем шаге. В фазе учета наблюдения информация об измерениях произведенных на текущем шаге используется для уточнения информации о состоянии системы, что делает её в результате (надеемся) более точной. | ||
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| + | |||
| + | ===Предсказание=== | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td width="50%"> | + | <td width="50%">Предсказанное состояние системы</td> |
<td> | <td> | ||
<math>\hat{\textbf{x}}_{k|k-1} = \textbf{F}_{k}\hat{\textbf{x}}_{k-1|k-1} + \textbf{B}_{k-1} \textbf{u}_{k-1} </math> | <math>\hat{\textbf{x}}_{k|k-1} = \textbf{F}_{k}\hat{\textbf{x}}_{k-1|k-1} + \textbf{B}_{k-1} \textbf{u}_{k-1} </math> | ||
| Строка 61: | Строка 90: | ||
<tr> | <tr> | ||
<td> | <td> | ||
| − | + | Оценка предсказания через матрицу ковариаций | |
</td> | </td> | ||
<td> | <td> | ||
| Строка 69: | Строка 98: | ||
</table> | </table> | ||
| − | === | + | |
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| + | |||
| + | ===Учет наблюдений=== | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td width="50%"> | + | <td width="50%">Отклонение наблюдения от ожидаемого</td> |
<td> | <td> | ||
<math> | <math> | ||
| Строка 81: | Строка 114: | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| − | <td> | + | <td>Матрица ковариаций отклонения</td> |
<td><math>\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k </math></td> | <td><math>\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| − | <td>'' | + | <td>''Оптимальная'' по Калману матрица коэффициентов усиления</td> |
<td><math>\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}</math></td> | <td><math>\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}</math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| − | <td> | + | <td>Обновлённая оценка состояния системы</td> |
<td><math>\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}^{-}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k</math></td> | <td><math>\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}^{-}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k</math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| − | <td> | + | <td>Обновлённая матрица ковариаций вычисленного состояния системы</td> |
<td><math>\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}</math></td> | <td><math>\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}</math></td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | |||
| − | === | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] |
| − | + | ||
| + | |||
| + | Формула для обновленной матрицы ковариаций состояния системы верна только для оптимальной по Калману матрицы '''K'''. Использование другой матрицы '''K''' требует более сложной формулы, которую можно найти ниже, в части ''вывод формул'' этой страницы. | ||
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| + | |||
| + | ===Инварианты=== | ||
| + | Если модель точна, и значения <math>\hat{\textbf{x}}_{0|0}</math> и <math>\textbf{P}_{0|0}</math> точно отражают функции распределения первоначальных значений вектора состояния системы, тогда следующие инварианты сохраняются после любого количества итераций фильтра Калмана: | ||
| + | |||
| + | Все оценки имеют нулевое матожидание погрешности: | ||
*<math>\textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0</math> | *<math>\textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0</math> | ||
*<math>\textrm{E}[\tilde{\textbf{y}}_k] = 0</math> | *<math>\textrm{E}[\tilde{\textbf{y}}_k] = 0</math> | ||
| − | + | где <math>\textrm{E}[\xi]</math> является матожиданием <math>\xi</math>, и кроме того: | |
| + | |||
| + | Все матрицы ковариаций точно отражают ковариации соответствующих величин: | ||
*<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k})</math> | *<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k})</math> | ||
*<math>\textbf{P}_{k|k-1} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})</math> | *<math>\textbf{P}_{k|k-1} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})</math> | ||
*<math>\textbf{S}_{k} = \textrm{cov}(\tilde{\textbf{y}}_k)</math> | *<math>\textbf{S}_{k} = \textrm{cov}(\tilde{\textbf{y}}_k)</math> | ||
| − | |||
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| + | |||
| + | |||
| + | == Примеры == | ||
| + | Рассмотрим грузовик на идеальной бесконечной дороге без трения. Изначально грузовик покоится в положении 0, но начинает двигаться со случайным ускорением. Мы измеряем его положение каждые ''Δt'' секунд, но эти измерения не точные; мы хотим поддерживать информацию о положении грузовика и его скорости. Сейчас мы покажем, как строить модель, из которой мы сможем создать фильтр Калмана для обработки результатов наших измерений. | ||
| + | |||
| + | Так как никакого управления в грузовике условиями задач не предусмотрено, мы будем игнорировать '''B'''<sub>''k''</sub> и '''u'''<sub>''k''</sub>. Кроме того '''F''', '''H''', '''R''' и '''Q''' являются константами, поэтому их индексы по времени мы тоже опустим. | ||
| − | + | Положение и скорость грузовика описываются линейным пространством состояний | |
:<math>\textbf{x}_{k} = \begin{bmatrix} x \\ \dot{x} \end{bmatrix} </math> | :<math>\textbf{x}_{k} = \begin{bmatrix} x \\ \dot{x} \end{bmatrix} </math> | ||
| − | + | где <math>\dot{x}</math> скорость, то есть первая производная положения по времени. | |
| − | + | Так же мы будем предполагать, что между моментами времени (''k'' − 1)<sup>th</sup> и ''k''<sup>th</sup> грузовик двигался с постоянным ускорением ''a''<sub>''k''</sub> которое нормально (по Гауссу) распределено, имеет нулевое матожидание и стандартное отклонение ''σ''<sub>''a''</sub>. Из трёх законов Ньютона мы знаем, что | |
:<math>\textbf{x}_{k} = \textbf{F} \textbf{x}_{k-1} + \textbf{G}a_{k}</math> | :<math>\textbf{x}_{k} = \textbf{F} \textbf{x}_{k-1} + \textbf{G}a_{k}</math> | ||
| − | + | где | |
:<math>\textbf{F} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix}</math> | :<math>\textbf{F} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix}</math> | ||
| − | + | и | |
:<math>\textbf{G} = \begin{bmatrix} \frac{\Delta t^{2}}{2} \\ \Delta t \end{bmatrix} </math> | :<math>\textbf{G} = \begin{bmatrix} \frac{\Delta t^{2}}{2} \\ \Delta t \end{bmatrix} </math> | ||
| − | + | Далее вычислим | |
:<math> \textbf{Q} = \textrm{cov}(\textbf{G}a) = \textrm{E}[(\textbf{G}a)(\textbf{G}a)^{\text{T}}] = \textbf{G} \textrm{E}[a^2] \textbf{G}^{\text{T}} = \textbf{G}[\sigma_a^2]\textbf{G}^{\text{T}} = \sigma_a^2 \textbf{G}\textbf{G}^{\text{T}}</math> (since ''σ''<sub>''a''</sub> is a scalar). | :<math> \textbf{Q} = \textrm{cov}(\textbf{G}a) = \textrm{E}[(\textbf{G}a)(\textbf{G}a)^{\text{T}}] = \textbf{G} \textrm{E}[a^2] \textbf{G}^{\text{T}} = \textbf{G}[\sigma_a^2]\textbf{G}^{\text{T}} = \sigma_a^2 \textbf{G}\textbf{G}^{\text{T}}</math> (since ''σ''<sub>''a''</sub> is a scalar). | ||
| − | + | На каждом шаге по времени производится неточное измерение положения грузовика. Давайте предположим, что эта погрешность так же нормально распределена с матожиданием 0 и стандартным отклонением ''σ''<sub>z</sub>. | |
:<math>\textbf{z}_{k} = \textbf{H x}_{k} + \textbf{v}_{k}</math> | :<math>\textbf{z}_{k} = \textbf{H x}_{k} + \textbf{v}_{k}</math> | ||
| − | + | где | |
:<math>\textbf{H} = \begin{bmatrix} 1 & 0 \end{bmatrix} </math> | :<math>\textbf{H} = \begin{bmatrix} 1 & 0 \end{bmatrix} </math> | ||
| − | + | и | |
:<math>\textbf{R} = \textrm{E}[\textbf{v}_k \textbf{v}_k^{\text{T}}] = \begin{bmatrix} \sigma_z^2 \end{bmatrix} </math> | :<math>\textbf{R} = \textrm{E}[\textbf{v}_k \textbf{v}_k^{\text{T}}] = \begin{bmatrix} \sigma_z^2 \end{bmatrix} </math> | ||
| − | + | Мы знаем начальное положение грузовика с идеальной точностью, поэтому инициализируем | |
:<math>\hat{\textbf{x}}_{0|0} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} </math> | :<math>\hat{\textbf{x}}_{0|0} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} </math> | ||
| − | + | и чтобы сказать фильтру, что мы знаем точное положение в начале работы, мы даём ему нулевую матрицу ковариаций: | |
:<math>\textbf{P}_{0|0} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} </math> | :<math>\textbf{P}_{0|0} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} </math> | ||
| − | + | Если начальное положение и скорость не известны с идеальной точностью, тогда можно инициализировать матрицу ковариаций достаточно большими числами, обозначенными ниже как ''B'', на её диагонали. | |
:<math>\textbf{P}_{0|0} = \begin{bmatrix} B & 0 \\ 0 & B \end{bmatrix} </math> | :<math>\textbf{P}_{0|0} = \begin{bmatrix} B & 0 \\ 0 & B \end{bmatrix} </math> | ||
| − | + | В этом случае фильтр Калмана предпочтет использовать информацию из первых измерений, чем выданную ему изначально информацию о состоянии системы. | |
| − | == | + | == Вывод формул == |
| − | === | + | === Вывод матрицы ковариаций с учетом наблюдений === |
| − | + | Начнем с инварианта, представляющего матрицу ковариаций погрешностей полученного состояния системы '''P'''<sub>''k''|''k''</sub> определенной выше как | |
:<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - \hat{\textbf{x}}_{k|k})</math> | :<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - \hat{\textbf{x}}_{k|k})</math> | ||
| − | + | подставим в него развёрнутое значение <math>\hat{\textbf{x}}_{k|k}</math> | |
:<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_{k}))</math> | :<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_{k}))</math> | ||
| − | + | и заменим <math>\tilde{\textbf{y}}_k</math> | |
:<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k(\textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1})))</math> | :<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k(\textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1})))</math> | ||
| − | + | и <math>\textbf{z}_{k}</math> | |
:<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k(\textbf{H}_k\textbf{x}_k + \textbf{v}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1})))</math> | :<math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k(\textbf{H}_k\textbf{x}_k + \textbf{v}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1})))</math> | ||
| − | + | вынеся отдельно вектор погрешности измерения '''v'''<sub>''k''</sub>, получаем | |
:<math>\textbf{P}_{k|k} = \textrm{cov}((I - \textbf{K}_k \textbf{H}_{k})(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}) - \textbf{K}_k \textbf{v}_k )</math> | :<math>\textbf{P}_{k|k} = \textrm{cov}((I - \textbf{K}_k \textbf{H}_{k})(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}) - \textbf{K}_k \textbf{v}_k )</math> | ||
| − | + | Так как '''v'''<sub>''k''</sub> не коррелирует с другими значениям в формуле, получаем | |
:<math>\textbf{P}_{k|k} = \textrm{cov}((I - \textbf{K}_k \textbf{H}_{k})(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})) + \textrm{cov}(\textbf{K}_k \textbf{v}_k )</math> | :<math>\textbf{P}_{k|k} = \textrm{cov}((I - \textbf{K}_k \textbf{H}_{k})(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})) + \textrm{cov}(\textbf{K}_k \textbf{v}_k )</math> | ||
| − | + | по свойствам ковариации вектора это преобразуется в | |
:<math>\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_{k})\textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})(I - \textbf{K}_k \textbf{H}_{k})^{\text{T}} + \textbf{K}_k\textrm{cov}(\textbf{v}_k )\textbf{K}_k^{\text{T}}</math> | :<math>\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_{k})\textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})(I - \textbf{K}_k \textbf{H}_{k})^{\text{T}} + \textbf{K}_k\textrm{cov}(\textbf{v}_k )\textbf{K}_k^{\text{T}}</math> | ||
| − | + | если теперь использовать наш инвариант '''P'''<sub>''k''|''k''-1</sub> и определение '''R'''<sub>''k''</sub>, то получим | |
:<math>\textbf{P}_{k|k} = | :<math>\textbf{P}_{k|k} = | ||
(I - \textbf{K}_k \textbf{H}_{k}) \textbf{P}_{k|k-1} (I - \textbf{K}_k \textbf{H}_{k})^\text{T} + | (I - \textbf{K}_k \textbf{H}_{k}) \textbf{P}_{k|k-1} (I - \textbf{K}_k \textbf{H}_{k})^\text{T} + | ||
\textbf{K}_k \textbf{R}_k \textbf{K}_k^\text{T} | \textbf{K}_k \textbf{R}_k \textbf{K}_k^\text{T} | ||
</math> | </math> | ||
| − | + | Эта формула (иногда называемая "'''формой Йосефа'''" для уравнения обновления ковариации) верна не зависимо от выбора матрицы '''K'''<sub>''k''</sub>. Однако если в качестве '''K'''<sub>''k''</sub> взята матрица оптимального по Калману коэффициента усиления, то её можно еще упростить, как это сделать мы расскажем ниже. | |
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| − | === | + | ===Вывод оптимальной матрицы коэффициентов усиления=== |
| − | + | Фильтр Калмана является фильтром, минимизирующим сумму квадратов матожидания погрешностей. Вектор погрешностей после корректировки оценочного состояния системы выглядит следующим образом | |
:<math>\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}</math> | :<math>\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}</math> | ||
| − | + | Мы будем минимизировать сумму квадратов матожидания координат этого вектора, <math>\textrm{E}[|\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}|^2]</math>. Это эквивалентно минимизации следа (суммы элементов на главной диагонали) матрицы ковариаций оценочного состояния системы после корректировки <math> \textbf{P}_{k|k} </math>. Подставив в это уравнение имеющиеся у нас формулы и проделав несколько преобразований, мы получаем: | |
:{| | :{| | ||
|- | |- | ||
| Строка 202: | Строка 255: | ||
|} | |} | ||
| − | + | След матрицы минимален, когда производная матрицы равна нулю: | |
:<math>\frac{\partial \; \textrm{tr}(\textbf{P}_{k|k})}{\partial \;\textbf{K}_k} = -2 (\textbf{H}_k \textbf{P}_{k|k-1})^\text{T} + 2 \textbf{K}_k \textbf{S}_k = 0</math> | :<math>\frac{\partial \; \textrm{tr}(\textbf{P}_{k|k})}{\partial \;\textbf{K}_k} = -2 (\textbf{H}_k \textbf{P}_{k|k-1})^\text{T} + 2 \textbf{K}_k \textbf{S}_k = 0</math> | ||
| − | + | Решая это уравнение относительно '''K'''<sub>''k''</sub> мы получаем оптимальный по Калману коэффициент усиления: | |
:<math>\textbf{K}_k \textbf{S}_k = (\textbf{H}_k \textbf{P}_{k|k-1})^\text{T} = \textbf{P}_{k|k-1} \textbf{H}_k^\text{T}</math> | :<math>\textbf{K}_k \textbf{S}_k = (\textbf{H}_k \textbf{P}_{k|k-1})^\text{T} = \textbf{P}_{k|k-1} \textbf{H}_k^\text{T}</math> | ||
| Строка 211: | Строка 264: | ||
:<math> \textbf{K}_{k} = \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} \textbf{S}_k^{-1}</math> | :<math> \textbf{K}_{k} = \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} \textbf{S}_k^{-1}</math> | ||
| − | + | Эта матрица, является искомой и минимизирует сумму квадратов матожидания координат вектора погрешности оценочного состояния системы. | |
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| − | === | + | === Упрощение для полученной скорректированной матрицы ковариаций === |
| − | + | Формула для расчета скорректированной матрицы ковариаций может быть упрощена, если в ней мы используем матрицу '''K'''<sub>''k''</sub> оптимальную по Калману (выведенную выше). Умножая обе стороны формулы вывода этой матрицы на '''S'''<sub>''k''</sub>'''K'''<sub>''k''</sub><sup>''T''</sup>, получаем | |
:<math>\textbf{K}_k \textbf{S}_k \textbf{K}_k^T = \textbf{P}_{k|k-1} \textbf{H}_k^T \textbf{K}_k^T</math> | :<math>\textbf{K}_k \textbf{S}_k \textbf{K}_k^T = \textbf{P}_{k|k-1} \textbf{H}_k^T \textbf{K}_k^T</math> | ||
| − | + | Если это подставить в нашу полную формулу для скорректированной матрицы ковариаций, получим | |
:<math> \textbf{P}_{k|k} = \textbf{P}_{k|k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} - \textbf{P}_{k|k-1} \textbf{H}_k^T \textbf{K}_k^T + \textbf{K}_k \textbf{S}_k \textbf{K}_k^T</math> | :<math> \textbf{P}_{k|k} = \textbf{P}_{k|k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} - \textbf{P}_{k|k-1} \textbf{H}_k^T \textbf{K}_k^T + \textbf{K}_k \textbf{S}_k \textbf{K}_k^T</math> | ||
| − | + | видно, что последние 2 слагаемых ликвидируются, и мы получаем | |
:<math> \textbf{P}_{k|k} = \textbf{P}_{k|k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} = (I - \textbf{K}_{k} \textbf{H}_{k}) \textbf{P}_{k|k-1}.</math> | :<math> \textbf{P}_{k|k} = \textbf{P}_{k|k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} = (I - \textbf{K}_{k} \textbf{H}_{k}) \textbf{P}_{k|k-1}.</math> | ||
| − | + | Эта формула значительно проще в смысле вычислительной сложности (объем вычислений требуемый для её применения) и практически всегда используется на практике, но она верна только для оптимального по Калману коэффициента усиления. Если точность арифметических операций необычайно мала и вызывает проблемы с [[:ru:Вычислительная устойчивость|вычислительной устройчивостью]], или если используется коэффициент усиления, отличный от оптимального по Калману, это упрощение не может быть применено и должна использоваться полная формула для скорректированной матрицы ковариаций. | |
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
== Relationship to the digital filter == | == Relationship to the digital filter == | ||
The Kalman filter can be regarded as an adaptive low-pass infinite impulse response [[digital filter]], with cut-off frequency depending on the ratio between the process- and measurement (or observation) noise, as well as the estimate covariance. Frequency response is, however, rarely of interest when designing state estimators such as the Kalman Filter, whereas for digital filters such as [[Infinite impulse response|IIR]] and [[Finite impulse response|FIR]] filters, frequency response is usually of primary concern. For the Kalman Filter, the important goal is how accurate the filter is, and this is most often decided based on empirical Monte Carlo simulations, where "truth" (the true state) is known. | The Kalman filter can be regarded as an adaptive low-pass infinite impulse response [[digital filter]], with cut-off frequency depending on the ratio between the process- and measurement (or observation) noise, as well as the estimate covariance. Frequency response is, however, rarely of interest when designing state estimators such as the Kalman Filter, whereas for digital filters such as [[Infinite impulse response|IIR]] and [[Finite impulse response|FIR]] filters, frequency response is usually of primary concern. For the Kalman Filter, the important goal is how accurate the filter is, and this is most often decided based on empirical Monte Carlo simulations, where "truth" (the true state) is known. | ||
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
== Relationship to [[recursive Bayesian estimation]] == | == Relationship to [[recursive Bayesian estimation]] == | ||
| Строка 270: | Строка 335: | ||
Note that the PDF at the previous timestep is inductively assumed to be the estimated state and covariance. This is justified because, as an optimal estimator, the Kalman filter makes best use of the measurements, therefore the PDF for <math>\mathbf{x}_k</math> given the measurements <math>\mathbf{Z}_k</math> ''is'' the Kalman filter estimate. | Note that the PDF at the previous timestep is inductively assumed to be the estimated state and covariance. This is justified because, as an optimal estimator, the Kalman filter makes best use of the measurements, therefore the PDF for <math>\mathbf{x}_k</math> given the measurements <math>\mathbf{Z}_k</math> ''is'' the Kalman filter estimate. | ||
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
==Information filter== | ==Information filter== | ||
| Строка 428: | Строка 497: | ||
** <math> \tilde{\textbf{K}}_k = \textbf{F}_k^{-1} \textbf{Q}_k \textbf{P}_{k+1|k}^{-1} </math> | ** <math> \tilde{\textbf{K}}_k = \textbf{F}_k^{-1} \textbf{Q}_k \textbf{P}_{k+1|k}^{-1} </math> | ||
| − | == | + | ==Нелинейные фильтры== |
| − | + | Изначально фильтр Калмана ограничен по области применения линейными системами. Однако большинство интересных для анализа систем являются нелинейными. Эта нелинейность может иметь отношение к модели процесса, к модели наблюдения или к обоим. | |
| + | |||
| + | |||
| + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | ||
| + | |||
| − | === | + | ===Расширенный фильтр Калмана (EKF) === |
| − | + | В расширенном фильтре Калмана, (extended Kalman filter, EKF) не требуется, чтобы модель состояния системы и модель наблюдения были линейными функциями, вместо этого требуется, чтобы они были дифференцируемы по состоянию системы. | |
| − | |||
:<math>\textbf{x}_{k} = f(\textbf{x}_{k-1}, \textbf{u}_{k}) + \textbf{w}_{k}</math> | :<math>\textbf{x}_{k} = f(\textbf{x}_{k-1}, \textbf{u}_{k}) + \textbf{w}_{k}</math> | ||
| Строка 439: | Строка 511: | ||
:<math>\textbf{z}_{k} = h(\textbf{x}_{k}) + \textbf{v}_{k}</math> | :<math>\textbf{z}_{k} = h(\textbf{x}_{k}) + \textbf{v}_{k}</math> | ||
| − | + | В этой модели функция ''f'' используется для расчета предсказываемого оценочного состояния системы из предыдущего и аналогично функция ''h'' используется для предсказываемого результата измерения из предсказанного состояния системы. Не смотря на то, что ''f'' и ''h'' не могут быть применены для расчета ковариаций напрямую, мы можем использовать вместо них соответствующие матрицы частных производных (Якобианы) в соответствующих точках (в предыдущем и предсказанном состояниях системы). | |
| − | + | На каждом шаге мы расчитываем эти Якобианы и просто подставляем их вместо матриц F и H в обычные формулы фильтра Калмана. Таким образом мы просто линеаризуем нелинейные функции ''f'' и ''h'' вблизи соответствующих точек, что допускается, т.к. они по объявленным в начале требованиям дифференцируемы. | |
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| + | |||
| + | |||
| + | ===Сигма-точечный фильтр (UKF)=== | ||
| + | |||
| + | Когда модели состояния системы и наблюдения, а значит и функции предсказания состояния системы и модели наблюдения <math>f</math> и <math>h</math> (см. выше) – в значительной степени нелинейны, расширенная версия фильтра Калмана может быть не эффективна.<ref name="JU97">{{cite journal | ||
| author = Julier, S.J. | | author = Julier, S.J. | ||
| coauthors = Uhlmann, J.K. | | coauthors = Uhlmann, J.K. | ||
| Строка 456: | Строка 532: | ||
}}</ref> This is because the mean and covariance are propagated through linearization of the underlying non-linear model. The '''unscented Kalman filter (UKF)''' <ref name="JU97"/> uses a deterministic sampling technique known as the [[unscented transform]] to pick a minimal set of sample points (called sigma points) around the mean. These sigma points are then propagated through the non-linear functions, from which the mean and covariance of the estimate are then recovered. The result is a filter which more accurately captures the true mean and covariance. (This can be verified using [[Monte Carlo sampling]] or through a Taylor series expansion of the posterior statistics.) In addition, this technique removes the requirement to explicitly calculate Jacobians, which for complex functions can be a difficult task in itself (i.e., requiring complicated derivatives if done analytically or being computationally costly if done numerically). | }}</ref> This is because the mean and covariance are propagated through linearization of the underlying non-linear model. The '''unscented Kalman filter (UKF)''' <ref name="JU97"/> uses a deterministic sampling technique known as the [[unscented transform]] to pick a minimal set of sample points (called sigma points) around the mean. These sigma points are then propagated through the non-linear functions, from which the mean and covariance of the estimate are then recovered. The result is a filter which more accurately captures the true mean and covariance. (This can be verified using [[Monte Carlo sampling]] or through a Taylor series expansion of the posterior statistics.) In addition, this technique removes the requirement to explicitly calculate Jacobians, which for complex functions can be a difficult task in itself (i.e., requiring complicated derivatives if done analytically or being computationally costly if done numerically). | ||
| − | ''' | + | '''Предсказание''' |
As with the EKF, the UKF prediction can be used independently from the UKF update, in combination with a linear (or indeed EKF) update, or vice versa. | As with the EKF, the UKF prediction can be used independently from the UKF update, in combination with a linear (or indeed EKF) update, or vice versa. | ||
| Строка 483: | Строка 559: | ||
|} | |} | ||
| − | + | где | |
:{| | :{| | ||
| Строка 490: | Строка 566: | ||
|} | |} | ||
| − | + | это ''i''-я колонка квадратного корня матрицы | |
:{| | :{| | ||
| Строка 497: | Строка 573: | ||
|} | |} | ||
| − | + | использующего определение: квадратный корень ''A'' матрицы ''B'' удовлетворяет условию | |
:{| | :{| | ||
| Строка 503: | Строка 579: | ||
|} | |} | ||
| − | + | Квадратный корень матрицы должен рассчитываться используя устойчивые эффективные числовые методы, такие как [[Cholesky decomposition]]. | |
The sigma points are propagated through the transition function ''f''. | The sigma points are propagated through the transition function ''f''. | ||
| Строка 524: | Строка 600: | ||
Typical values for <math>\alpha</math>, <math>\beta</math>, and <math>\kappa</math> are <math>10^{-3}</math>, 2 and 0 respectively. (These values should suffice for most purposes.){{Fact|date=April 2009}} | Typical values for <math>\alpha</math>, <math>\beta</math>, and <math>\kappa</math> are <math>10^{-3}</math>, 2 and 0 respectively. (These values should suffice for most purposes.){{Fact|date=April 2009}} | ||
| − | ''' | + | '''Учет наблюдений''' |
The predicted state and covariance are augmented as before, except now with the mean and covariance of the measurement noise. | The predicted state and covariance are augmented as before, except now with the mean and covariance of the measurement noise. | ||
| Строка 553: | Строка 629: | ||
:<math> \chi_{k|k-1} := [ \chi_{k|k-1}^T \quad E[\textbf{v}_{k}^{T}] \ ]^{T} \pm \sqrt{ (L + \lambda) \textbf{R}_{k}^{a} }</math> | :<math> \chi_{k|k-1} := [ \chi_{k|k-1}^T \quad E[\textbf{v}_{k}^{T}] \ ]^{T} \pm \sqrt{ (L + \lambda) \textbf{R}_{k}^{a} }</math> | ||
| − | + | где | |
:<math> \textbf{R}_{k}^{a} = \begin{bmatrix} & 0 & & 0 & \\ & 0 & &\textbf{R}_{k} & \end{bmatrix} </math> | :<math> \textbf{R}_{k}^{a} = \begin{bmatrix} & 0 & & 0 & \\ & 0 & &\textbf{R}_{k} & \end{bmatrix} </math> | ||
| Строка 583: | Строка 659: | ||
:<math>\textbf{P}_{k|k} = \textbf{P}_{k|k-1} - K_{k} \textbf{P}_{z_{k}z_{k}} K_{k}^{T} </math> | :<math>\textbf{P}_{k|k} = \textbf{P}_{k|k-1} - K_{k} \textbf{P}_{z_{k}z_{k}} K_{k}^{T} </math> | ||
| − | |||
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| + | |||
| + | |||
| + | ==Фильтр Калмана-Бьюси== | ||
| + | Фильтр Калмана-Бьюси это непрерывная версия фильтра Калмана .<ref>Bucy, R.S. and Joseph, P.D., ''Filtering for Stochastic Processes with Applications to Guidance,'' John Wiley & Sons, 1968; 2nd Edition, AMS Chelsea Publ., 2005. ISBN 0821837826</ref><ref>Jazwinski, Andrew H., ''Stochastic processes and filtering theory,'' Academic Press, New York, 1970. ISBN 0123815509 </ref> | ||
| + | |||
| + | Он основан на следующей модели пространства состояний системы | ||
:<math>\frac{d}{dt}\mathbf{x}(t) = \mathbf{F}(t)\mathbf{x}(t) + \mathbf{w}(t)</math> | :<math>\frac{d}{dt}\mathbf{x}(t) = \mathbf{F}(t)\mathbf{x}(t) + \mathbf{w}(t)</math> | ||
| Строка 592: | Строка 672: | ||
:<math>\mathbf{z}(t) = \mathbf{H}(t) \mathbf{x}(t) + \mathbf{v}(t)</math> | :<math>\mathbf{z}(t) = \mathbf{H}(t) \mathbf{x}(t) + \mathbf{v}(t)</math> | ||
| − | + | где матрицами ковариаций погрешностей <math>\mathbf{w}(t)</math> и <math>\mathbf{v}(t)</math> являются <math>\mathbf{Q}(t)</math> и <math>\mathbf{R}(t)</math>, соответственно. | |
| − | + | Фильтр состоит из двух дифференциальных уравнений, одно для функции оценочного состояния системы, а второе для функции матрицы ковариаций этого состояния: | |
:<math>\frac{d}{dt}\hat{\mathbf{x}}(t) = \mathbf{F}(t)\hat{\mathbf{x}}(t) + \mathbf{K}(t) (\mathbf{z}(t)-\mathbf{H}(t)\hat{\mathbf{x}}(t))</math> | :<math>\frac{d}{dt}\hat{\mathbf{x}}(t) = \mathbf{F}(t)\hat{\mathbf{x}}(t) + \mathbf{K}(t) (\mathbf{z}(t)-\mathbf{H}(t)\hat{\mathbf{x}}(t))</math> | ||
| Строка 600: | Строка 680: | ||
:<math>\frac{d}{dt}\mathbf{P}(t) = \mathbf{F}(t)\mathbf{P}(t) + \mathbf{P}(t)\mathbf{F}^{T}(t) + \mathbf{Q}(t) - \mathbf{K}(t)\mathbf{R}(t)\mathbf{K}^{T}(t)</math> | :<math>\frac{d}{dt}\mathbf{P}(t) = \mathbf{F}(t)\mathbf{P}(t) + \mathbf{P}(t)\mathbf{F}^{T}(t) + \mathbf{Q}(t) - \mathbf{K}(t)\mathbf{R}(t)\mathbf{K}^{T}(t)</math> | ||
| − | + | где коэффициент усиления Калмана определен, как | |
:<math>\mathbf{K}(t)=\mathbf{P}(t)\mathbf{H}^{T}(t)\mathbf{R}^{-1}(t)</math> | :<math>\mathbf{K}(t)=\mathbf{P}(t)\mathbf{H}^{T}(t)\mathbf{R}^{-1}(t)</math> | ||
| − | + | Обратите внимение, что в выражении для <math>\mathbf{K}(t)</math> матрица ковариаций погрешности наблюдения <math>\mathbf{R}(t)</math> является одновременно матрицей ковариаций ошибки корректировки вектора состояния системы <math>\tilde{\mathbf{y}}(t)=\mathbf{z}(t)-\mathbf{H}(t)\hat{\mathbf{x}}(t)</math>; эти ковариации совпадают только в непрерывном случае.<ref>Kailath, Thomas, "An innovation approach to least-squares estimation Part I: Linear filtering in additive white noise", ''IEEE Transactions on Automatic Control'', 13(6), 646-655, 1968</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | В непрерывном случае отсутствуют отдельные шаги для расчета результата управляющего воздействия и внесения информации о результатах наблюдений, которые можно выделить для дискретной по времени модели. | ||
| − | + | Второе дифференциальное уравнение для ковариаций является примером уравнения Риккати. | |
| − | |||
| − | |||
| − | |||
| − | + | '''Source(s):''' [http://www.downloadranking.com Фильтр Калмана] | |
| − | |||
| − | + | == Сноски == | |
| + | <references /> | ||
Текущая версия на 10:08, 22 марта 2013
Авторство исходной статьи коллективное
Перевод: © Ботов Антон aka =DeaD=, 2009
Эксклюзивно для www.roboforum.ru
копирование на другие ресурсы и публикация перевода
без разрешения его автора запрещены
Фильтр Калмана это эффективный рекурсивный фильтр, который оценивает состояние линейной динамической системы по серии неточных измерений. Он используется в широком спектре задач от радаров до систем технического зрения, и является важной частью теории управления системами.
Source(s): Фильтр Калмана
Содержание
- 1 Примеры решаемых фильтром задач
- 2 Используемая модель динамической системы
- 3 Фильтр Калмана
- 4 Примеры
- 5 Вывод формул
- 6 Relationship to the digital filter
- 7 Relationship to recursive Bayesian estimation
- 8 Information filter
- 9 Fixed-lag smoother
- 10 Fixed-interval filters
- 11 Нелинейные фильтры
- 12 Фильтр Калмана-Бьюси
- 13 Сноски
Примеры решаемых фильтром задач
В качестве примера можно привести предоставление точной, поддерживаемой в актуальном состоянии, информации о положении и скорости объекта, при наличии серии измерений положения объекта, каждое из которых в некоторой степени неточно. Например, в радарах при отслеживании цели мы имеем очень зашумлённую (неточную) информацию о положении, скорости и ускорении наблюдаемого объекта. Фильтр Калмана использует известную нам математическую модель динамики объекта, которая описывает какие вообще изменения состояния объекта возможны, чтобы устранить погрешности измерения и предоставить хорошей точности положение объекта в данный момент (фильтрация), в будущие моменты (предсказание), или в какие-то из прошедших моментов (интерполяция или сглаживание).
В качестве альтернативного примера рассмотрим старый тихоходный автомобиль, про который точно известно, что он разгоняется от 0 до 100км/ч не менее чем за 10 секунд. Представим, что спидометр этого автомобиля барахлит и показывает скорость с погрешностью 60км/ч от настоящей. Из неподвижного положения, которое измерено точно, потому что колёса не вращались, водитель нажимает педаль газа в пол и через 5 секунд спидометр показывает 110км/ч, но водитель то знает, что машина не может так быстро разогнаться, поэтому он использует информацию о погрешности и понимает, что сейчас скорее всего, учитывая то, что он знает на сколько может врать спидометр, скорость около 50км/ч. Так же и фильтр Калмана использует информацию о погрешности измерений и о том, каким правилам подчиняется динамическая система, для минимизации погрешности измерений и предоставления максимально точной информации о состоянии системы.
Наглядные примеры в сети:
Source(s): Фильтр Калмана
Используемая модель динамической системы
Фильтры Калмана основываются на линейных динамических системах, дискретизированных по времени. Они моделируются цепями Маркова, построенными на линейных операторах с внесенными погрешностями с нормальным Гауссовым распределением. Состояние системы считается вектор из действительных чисел. При каждом шаге по времени, линейный оператор применяется к вектору состояния системы, добавляется некоторая погрешность и опционально некоторая информация об управляющих воздействиях на систему, если таковая известна. После чего другим линейным оператором с другой погрешностью добавляется видимая информация о состоянии системы. Фильтр Калмана можно рассматривать в качестве аналога скрытым моделям Маркова, с тем ключевым отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут работать с произвольными распределениями для следующих значений переменных состояния системы, в отличие от модели стандартного Гауссового распределения, поддерживаемого фильтрами Калмана. Существует строгая взаимосвязь между уравнениями фильтра Калмана и аналогичными в скрытых моделях Маркова. Подробней эта тема, как и некоторые другие модели, рассмотрена авторами Roweis и Ghahramani (1999).[1]
Чтобы было возможным использовать фильтр Калмана для оценки внутреннего состояния системы по серии неточных измерений, необходимо представить модель данного процесса в соответствии с универсальной моделью процесс для фильтра Калмана. Это означает, что нужно указать матрицы Fk, Hk, Qk, Rk, и иногда Bk для каждого шага по времени k, как указано ниже.
Source(s): Фильтр Калмана
Модель системы для фильтра Калмана подразумевает, что реальное состояние в момент времени k получается из состояния в момент времени (k − 1) по правилу:
<math> \textbf{x}_{k} = \textbf{F}_{k} \textbf{x}_{k-1} + \textbf{B}_{k} \textbf{u}_{k} + \textbf{w}_{k} </math>,
где
- Fk матрица соответствующая модели преобразованию системы со временем, применяемая к предыдущему состоянию xk−1;
- Bk матрица соответствующая модели применения управляющего воздействия, которая применяется к состоянию системы умноженная на вектор управляющего воздействия uk;
- wk вектор погрешности, которая предполагается, имеет нулевое матожидание, нормальное Гауссово распределение и матрицу ковариаций Qk:
<math>\textbf{w}_{k} \sim N(0, \textbf{Q}_k) </math>
В момент времени k производится наблюдение (или измерение) zk реального состояния системы xk в соответствии с моделью измерения
- <math>\textbf{z}_{k} = \textbf{H}_{k} \textbf{x}_{k} + \textbf{v}_{k}</math>
где Hk матрица, соответствующая модели наблюдения, которая отображает пространство векторов реального состояния системы в пространство векторов результатов наблюдений, а vk это вектор ошибки наблюдения, который считается имеющим нулевое матожидание, нормальное Гауссово распределение и матрицу ковариаций Rk:
<math>\textbf{v}_{k} \sim N(0, \textbf{R}_k) </math>
Вектор начального состояния системы и векторы погрешностей на каждом шаге {x0, w1, ..., wk, v1 ... vk} считаются не зависящими друг от друга.
Множество реальных динамических систем не полностью вписываются в эту модель, однако по причине того, что фильтр Калмана предназначен для работы в ситуации неточных данных, ответы, генерируемые этим фильтром, часто являются очень хорошим приближением к правильному ответу, что делает фильтр очень полезным даже в таких ситуациях. Вариации Калмановской фильтрации описанные ниже позволяют работать с более сложными моделями.
Source(s): Фильтр Калмана
Фильтр Калмана
Фильтр Калмана является разновидностью рекурсивного фильтра. Это означает, что только результат предыдущей итерации фильтра (в виде оценки состояния системы и оценки погрешности определения этого состояния) и текущие наблюдения нужны для расчета текущего состояния системы. В отличие от пакетных фильтров не требуется хранение никакой истории наблюдений. В следующем дальше тексте запись <math>\hat{\textbf{x}}_{n|m}</math> означает оценку состояния системы <math>\textbf{x}</math> в момент времени n при учете наблюдений (измерений) с начала работы фильтра и по момент времени m включительно.
Состояние фильтра содержится в двух переменных:
- <math>\hat{\textbf{x}}_{k|k}</math>, оценочное состояние системы в момент времени k, которое получено на основании начального состояния системы и всех наблюдений по момент времени k включительно;
- <math>\textbf{P}_{k|k}</math>, матрица ковариаций этого состояния, включающая в себя оценку дисперсий погрешности вычисленного состояния и уровни ковариаций, показывающих выявленные взаимосвязи между параметрами состояния системы.
Итерация фильтра Калмана делится на две фазы: Предсказание и Учет наблюдений. Фаза предсказания использует вычисленное на предыдущем шаге состояние для получения через модель системы оценочного состояния на текущем шаге. В фазе учета наблюдения информация об измерениях произведенных на текущем шаге используется для уточнения информации о состоянии системы, что делает её в результате (надеемся) более точной.
Source(s): Фильтр Калмана
Предсказание
| Предсказанное состояние системы |
<math>\hat{\textbf{x}}_{k|k-1} = \textbf{F}_{k}\hat{\textbf{x}}_{k-1|k-1} + \textbf{B}_{k-1} \textbf{u}_{k-1} </math> |
|
Оценка предсказания через матрицу ковариаций |
<math>\textbf{P}_{k|k-1} = \textbf{F}_{k} \textbf{P}_{k-1|k-1} \textbf{F}_{k}^{\text{T}} + \textbf{Q}_{k-1} </math> |
Source(s): Фильтр Калмана
Учет наблюдений
| Отклонение наблюдения от ожидаемого |
<math> \tilde{\textbf{y}}_k = \textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1} </math> |
| Матрица ковариаций отклонения | <math>\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k </math> |
| Оптимальная по Калману матрица коэффициентов усиления | <math>\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}</math> |
| Обновлённая оценка состояния системы | <math>\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}^{-}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k</math> |
| Обновлённая матрица ковариаций вычисленного состояния системы | <math>\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}</math> |
Source(s): Фильтр Калмана
Формула для обновленной матрицы ковариаций состояния системы верна только для оптимальной по Калману матрицы K. Использование другой матрицы K требует более сложной формулы, которую можно найти ниже, в части вывод формул этой страницы.
Source(s): Фильтр Калмана
Инварианты
Если модель точна, и значения <math>\hat{\textbf{x}}_{0|0}</math> и <math>\textbf{P}_{0|0}</math> точно отражают функции распределения первоначальных значений вектора состояния системы, тогда следующие инварианты сохраняются после любого количества итераций фильтра Калмана:
Все оценки имеют нулевое матожидание погрешности:
- <math>\textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0</math>
- <math>\textrm{E}[\tilde{\textbf{y}}_k] = 0</math>
где <math>\textrm{E}[\xi]</math> является матожиданием <math>\xi</math>, и кроме того:
Все матрицы ковариаций точно отражают ковариации соответствующих величин:
- <math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k})</math>
- <math>\textbf{P}_{k|k-1} = \textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})</math>
- <math>\textbf{S}_{k} = \textrm{cov}(\tilde{\textbf{y}}_k)</math>
Source(s): Фильтр Калмана
Примеры
Рассмотрим грузовик на идеальной бесконечной дороге без трения. Изначально грузовик покоится в положении 0, но начинает двигаться со случайным ускорением. Мы измеряем его положение каждые Δt секунд, но эти измерения не точные; мы хотим поддерживать информацию о положении грузовика и его скорости. Сейчас мы покажем, как строить модель, из которой мы сможем создать фильтр Калмана для обработки результатов наших измерений.
Так как никакого управления в грузовике условиями задач не предусмотрено, мы будем игнорировать Bk и uk. Кроме того F, H, R и Q являются константами, поэтому их индексы по времени мы тоже опустим.
Положение и скорость грузовика описываются линейным пространством состояний
- <math>\textbf{x}_{k} = \begin{bmatrix} x \\ \dot{x} \end{bmatrix} </math>
где <math>\dot{x}</math> скорость, то есть первая производная положения по времени.
Так же мы будем предполагать, что между моментами времени (k − 1)th и kth грузовик двигался с постоянным ускорением ak которое нормально (по Гауссу) распределено, имеет нулевое матожидание и стандартное отклонение σa. Из трёх законов Ньютона мы знаем, что
- <math>\textbf{x}_{k} = \textbf{F} \textbf{x}_{k-1} + \textbf{G}a_{k}</math>
где
- <math>\textbf{F} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix}</math>
и
- <math>\textbf{G} = \begin{bmatrix} \frac{\Delta t^{2}}{2} \\ \Delta t \end{bmatrix} </math>
Далее вычислим
- <math> \textbf{Q} = \textrm{cov}(\textbf{G}a) = \textrm{E}[(\textbf{G}a)(\textbf{G}a)^{\text{T}}] = \textbf{G} \textrm{E}[a^2] \textbf{G}^{\text{T}} = \textbf{G}[\sigma_a^2]\textbf{G}^{\text{T}} = \sigma_a^2 \textbf{G}\textbf{G}^{\text{T}}</math> (since σa is a scalar).
На каждом шаге по времени производится неточное измерение положения грузовика. Давайте предположим, что эта погрешность так же нормально распределена с матожиданием 0 и стандартным отклонением σz.
- <math>\textbf{z}_{k} = \textbf{H x}_{k} + \textbf{v}_{k}</math>
где
- <math>\textbf{H} = \begin{bmatrix} 1 & 0 \end{bmatrix} </math>
и
- <math>\textbf{R} = \textrm{E}[\textbf{v}_k \textbf{v}_k^{\text{T}}] = \begin{bmatrix} \sigma_z^2 \end{bmatrix} </math>
Мы знаем начальное положение грузовика с идеальной точностью, поэтому инициализируем
- <math>\hat{\textbf{x}}_{0|0} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} </math>
и чтобы сказать фильтру, что мы знаем точное положение в начале работы, мы даём ему нулевую матрицу ковариаций:
- <math>\textbf{P}_{0|0} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} </math>
Если начальное положение и скорость не известны с идеальной точностью, тогда можно инициализировать матрицу ковариаций достаточно большими числами, обозначенными ниже как B, на её диагонали.
- <math>\textbf{P}_{0|0} = \begin{bmatrix} B & 0 \\ 0 & B \end{bmatrix} </math>
В этом случае фильтр Калмана предпочтет использовать информацию из первых измерений, чем выданную ему изначально информацию о состоянии системы.
Вывод формул
Вывод матрицы ковариаций с учетом наблюдений
Начнем с инварианта, представляющего матрицу ковариаций погрешностей полученного состояния системы Pk|k определенной выше как
- <math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - \hat{\textbf{x}}_{k|k})</math>
подставим в него развёрнутое значение <math>\hat{\textbf{x}}_{k|k}</math>
- <math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_{k}))</math>
и заменим <math>\tilde{\textbf{y}}_k</math>
- <math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k(\textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1})))</math>
и <math>\textbf{z}_{k}</math>
- <math>\textbf{P}_{k|k} = \textrm{cov}(\textbf{x}_{k} - (\hat{\textbf{x}}_{k|k-1} + \textbf{K}_k(\textbf{H}_k\textbf{x}_k + \textbf{v}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1})))</math>
вынеся отдельно вектор погрешности измерения vk, получаем
- <math>\textbf{P}_{k|k} = \textrm{cov}((I - \textbf{K}_k \textbf{H}_{k})(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}) - \textbf{K}_k \textbf{v}_k )</math>
Так как vk не коррелирует с другими значениям в формуле, получаем
- <math>\textbf{P}_{k|k} = \textrm{cov}((I - \textbf{K}_k \textbf{H}_{k})(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})) + \textrm{cov}(\textbf{K}_k \textbf{v}_k )</math>
по свойствам ковариации вектора это преобразуется в
- <math>\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_{k})\textrm{cov}(\textbf{x}_k - \hat{\textbf{x}}_{k|k-1})(I - \textbf{K}_k \textbf{H}_{k})^{\text{T}} + \textbf{K}_k\textrm{cov}(\textbf{v}_k )\textbf{K}_k^{\text{T}}</math>
если теперь использовать наш инвариант Pk|k-1 и определение Rk, то получим
- <math>\textbf{P}_{k|k} =
(I - \textbf{K}_k \textbf{H}_{k}) \textbf{P}_{k|k-1} (I - \textbf{K}_k \textbf{H}_{k})^\text{T} + \textbf{K}_k \textbf{R}_k \textbf{K}_k^\text{T} </math> Эта формула (иногда называемая "формой Йосефа" для уравнения обновления ковариации) верна не зависимо от выбора матрицы Kk. Однако если в качестве Kk взята матрица оптимального по Калману коэффициента усиления, то её можно еще упростить, как это сделать мы расскажем ниже.
Source(s): Фильтр Калмана
Вывод оптимальной матрицы коэффициентов усиления
Фильтр Калмана является фильтром, минимизирующим сумму квадратов матожидания погрешностей. Вектор погрешностей после корректировки оценочного состояния системы выглядит следующим образом
- <math>\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}</math>
Мы будем минимизировать сумму квадратов матожидания координат этого вектора, <math>\textrm{E}[|\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}|^2]</math>. Это эквивалентно минимизации следа (суммы элементов на главной диагонали) матрицы ковариаций оценочного состояния системы после корректировки <math> \textbf{P}_{k|k} </math>. Подставив в это уравнение имеющиеся у нас формулы и проделав несколько преобразований, мы получаем:
k} </math> k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} - \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} \textbf{K}_k^\text{T} + \textbf{K}_k (\textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k) \textbf{K}_k^\text{T}</math> k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} - \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} \textbf{K}_k^\text{T} + \textbf{K}_k \textbf{S}_k\textbf{K}_k^\text{T}</math>
След матрицы минимален, когда производная матрицы равна нулю:
- <math>\frac{\partial \; \textrm{tr}(\textbf{P}_{k|k})}{\partial \;\textbf{K}_k} = -2 (\textbf{H}_k \textbf{P}_{k|k-1})^\text{T} + 2 \textbf{K}_k \textbf{S}_k = 0</math>
Решая это уравнение относительно Kk мы получаем оптимальный по Калману коэффициент усиления:
- <math>\textbf{K}_k \textbf{S}_k = (\textbf{H}_k \textbf{P}_{k|k-1})^\text{T} = \textbf{P}_{k|k-1} \textbf{H}_k^\text{T}</math>
- <math> \textbf{K}_{k} = \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} \textbf{S}_k^{-1}</math>
Эта матрица, является искомой и минимизирует сумму квадратов матожидания координат вектора погрешности оценочного состояния системы.
Source(s): Фильтр Калмана
Упрощение для полученной скорректированной матрицы ковариаций
Формула для расчета скорректированной матрицы ковариаций может быть упрощена, если в ней мы используем матрицу Kk оптимальную по Калману (выведенную выше). Умножая обе стороны формулы вывода этой матрицы на SkKkT, получаем
- <math>\textbf{K}_k \textbf{S}_k \textbf{K}_k^T = \textbf{P}_{k|k-1} \textbf{H}_k^T \textbf{K}_k^T</math>
Если это подставить в нашу полную формулу для скорректированной матрицы ковариаций, получим
- <math> \textbf{P}_{k|k} = \textbf{P}_{k|k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} - \textbf{P}_{k|k-1} \textbf{H}_k^T \textbf{K}_k^T + \textbf{K}_k \textbf{S}_k \textbf{K}_k^T</math>
видно, что последние 2 слагаемых ликвидируются, и мы получаем
- <math> \textbf{P}_{k|k} = \textbf{P}_{k|k-1} - \textbf{K}_k \textbf{H}_k \textbf{P}_{k|k-1} = (I - \textbf{K}_{k} \textbf{H}_{k}) \textbf{P}_{k|k-1}.</math>
Эта формула значительно проще в смысле вычислительной сложности (объем вычислений требуемый для её применения) и практически всегда используется на практике, но она верна только для оптимального по Калману коэффициента усиления. Если точность арифметических операций необычайно мала и вызывает проблемы с вычислительной устройчивостью, или если используется коэффициент усиления, отличный от оптимального по Калману, это упрощение не может быть применено и должна использоваться полная формула для скорректированной матрицы ковариаций.
Source(s): Фильтр Калмана
Relationship to the digital filter
The Kalman filter can be regarded as an adaptive low-pass infinite impulse response digital filter, with cut-off frequency depending on the ratio between the process- and measurement (or observation) noise, as well as the estimate covariance. Frequency response is, however, rarely of interest when designing state estimators such as the Kalman Filter, whereas for digital filters such as IIR and FIR filters, frequency response is usually of primary concern. For the Kalman Filter, the important goal is how accurate the filter is, and this is most often decided based on empirical Monte Carlo simulations, where "truth" (the true state) is known.
Source(s): Фильтр Калмана
Relationship to recursive Bayesian estimation
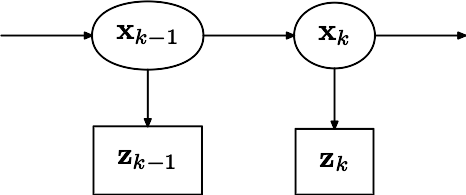
The true state is assumed to be an unobserved Markov process, and the measurements are the observed states of a hidden Markov model.
Because of the Markov assumption, the true state is conditionally independent of all earlier states given the immediately previous state.
- <math>p(\textbf{x}_k|\textbf{x}_0,\dots,\textbf{x}_{k-1}) = p(\textbf{x}_k|\textbf{x}_{k-1})</math>
Similarly the measurement at the k-th timestep is dependent only upon the current state and is conditionally independent of all other states given the current state.
- <math>p(\textbf{z}_k|\textbf{x}_0,\dots,\textbf{x}_{k}) = p(\textbf{z}_k|\textbf{x}_{k} )</math>
Using these assumptions the probability distribution over all states of the hidden Markov model can be written simply as:
- <math>p(\textbf{x}_0,\dots,\textbf{x}_k,\textbf{z}_1,\dots,\textbf{z}_k) = p(\textbf{x}_0)\prod_{i=1}^k p(\textbf{z}_i|\textbf{x}_i)p(\textbf{x}_i|\textbf{x}_{i-1})</math>
However, when the Kalman filter is used to estimate the state x, the probability distribution of interest is that associated with the current states conditioned on the measurements up to the current timestep. (This is achieved by marginalizing out the previous states and dividing by the probability of the measurement set.)
This leads to the predict and update steps of the Kalman filter written probabilistically. The probability distribution associated with the predicted state is the sum (integral) of the products of the probability distribution associated with the transition from the (k - 1)-th timestep to the k-th and the probability distribution associated with the previous state, over all possible <math>x_{k_-1}</math>.
- <math> p(\textbf{x}_k|\textbf{Z}_{k-1}) = \int p(\textbf{x}_k | \textbf{x}_{k-1}) p(\textbf{x}_{k-1} | \textbf{Z}_{k-1} ) \, d\textbf{x}_{k-1} </math>
The measurement set up to time t is
- <math> \textbf{Z}_{t} = \left \{ \textbf{z}_{1},\dots,\textbf{z}_{t} \right \} </math>
The probability distribution of the update is proportional to the product of the measurement likelihood and the predicted state.
- <math> p(\textbf{x}_k|\textbf{Z}_{k}) = \frac{p(\textbf{z}_k|\textbf{x}_k) p(\textbf{x}_k|\textbf{Z}_{k-1})}{p(\textbf{z}_k|\textbf{Z}_{k-1})} </math>
The denominator
- <math>p(\textbf{z}_k|\textbf{Z}_{k-1}) = \int p(\textbf{z}_k|\textbf{x}_k) p(\textbf{x}_k|\textbf{Z}_{k-1}) d\textbf{x}_k</math>
is a normalization term.
The remaining probability density functions are
- <math> p(\textbf{x}_k | \textbf{x}_{k-1}) = N(\textbf{F}_k\textbf{x}_{k-1}, \textbf{Q}_k)</math>
- <math> p(\textbf{z}_k|\textbf{x}_k) = N(\textbf{H}_{k}\textbf{x}_k, \textbf{R}_k) </math>
- <math> p(\textbf{x}_{k-1}|\textbf{Z}_{k-1}) = N(\hat{\textbf{x}}_{k-1},\textbf{P}_{k-1} )</math>
Note that the PDF at the previous timestep is inductively assumed to be the estimated state and covariance. This is justified because, as an optimal estimator, the Kalman filter makes best use of the measurements, therefore the PDF for <math>\mathbf{x}_k</math> given the measurements <math>\mathbf{Z}_k</math> is the Kalman filter estimate.
Source(s): Фильтр Калмана
Information filter
In the information filter, or inverse covariance filter, the estimated covariance and estimated state are replaced by the information matrix and information vector respectively. These are defined as:
- <math>\textbf{Y}_{k|k} = \textbf{P}_{k|k}^{-1} </math>
- <math>\hat{\textbf{y}}_{k|k} = \textbf{P}_{k|k}^{-1}\hat{\textbf{x}}_{k|k} </math>
Similarly the predicted covariance and state have equivalent information forms, defined as:
- <math>\textbf{Y}_{k|k-1} = \textbf{P}_{k|k-1}^{-1} </math>
- <math>\hat{\textbf{y}}_{k|k-1} = \textbf{P}_{k|k-1}^{-1}\hat{\textbf{x}}_{k|k-1} </math>
as have the measurement covariance and measurement vector, which are defined as:
- <math>\textbf{I}_{k} = \textbf{H}_{k}^{\text{T}} \textbf{R}_{k}^{-1} \textbf{H}_{k} </math>
- <math>\textbf{i}_{k} = \textbf{H}_{k}^{\text{T}} \textbf{R}_{k}^{-1} \textbf{z}_{k} </math>
The information update now becomes a trivial sum.
- <math>\textbf{Y}_{k|k} = \textbf{Y}_{k|k-1} + \textbf{I}_{k}</math>
- <math>\hat{\textbf{y}}_{k|k} = \hat{\textbf{y}}_{k|k-1} + \textbf{i}_{k}</math>
The main advantage of the information filter is that N measurements can be filtered at each timestep simply by summing their information matrices and vectors.
- <math>\textbf{Y}_{k|k} = \textbf{Y}_{k|k-1} + \sum_{j=1}^N \textbf{I}_{k,j}</math>
- <math>\hat{\textbf{y}}_{k|k} = \hat{\textbf{y}}_{k|k-1} + \sum_{j=1}^N \textbf{i}_{k,j}</math>
To predict the information filter the information matrix and vector can be converted back to their state space equivalents, or alternatively the information space prediction can be used.
- <math>\textbf{M}_{k} =
[\textbf{F}_{k}^{-1}]^{\text{T}} \textbf{Y}_{k-1|k-1} \textbf{F}_{k}^{-1} </math>
- <math>\textbf{C}_{k} =
\textbf{M}_{k} [\textbf{M}_{k}+\textbf{Q}_{k}^{-1}]^{-1}</math>
- <math>\textbf{L}_{k} =
I - \textbf{C}_{k} </math>
- <math>\textbf{Y}_{k|k-1} =
\textbf{L}_{k} \textbf{M}_{k} \textbf{L}_{k}^{\text{T}} +
\textbf{C}_{k} \textbf{Q}_{k}^{-1} \textbf{C}_{k}^{\text{T}}</math>
- <math>\hat{\textbf{y}}_{k|k-1} =
\textbf{L}_{k} [\textbf{F}_{k}^{-1}]^{\text{T}}\hat{\textbf{y}}_{k-1|k-1} </math>
Note that if F and Q are time invariant these values can be cached. Note also that F and Q need to be invertible.
Fixed-lag smoother
The optimal fixed-lag smoother provides the optimal estimate of <math>\hat{\textbf{x}}_{k - N | k}</math> for a given fixed-lag <math>N</math> using the measurements from <math>\textbf{z}_{1}</math> to <math>\textbf{z}_{k}</math>. It can be derived using the previous theory via an augmented state, and the main equation of the filter is the following:
<math> \begin{bmatrix} \hat{\textbf{x}}_{t|t} \\ \hat{\textbf{x}}_{t-1|t} \\ \vdots \\ \hat{\textbf{x}}_{t-N+1|t} \\ \end{bmatrix} = \begin{bmatrix} I \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \hat{\textbf{x}}_{t|t-1} + \begin{bmatrix} 0 & \ldots & 0 \\ I & 0 & \vdots \\ \vdots & \ddots & \vdots \\ 0 & \ldots & I \\ \end{bmatrix} \begin{bmatrix} \hat{\textbf{x}}_{t-1|t-1} \\ \hat{\textbf{x}}_{t-2|t-1} \\ \vdots \\ \hat{\textbf{x}}_{t-N|t-1} \\ \end{bmatrix} + \begin{bmatrix} K^{(1)} \\ K^{(2)} \\ \vdots \\ K^{(N)} \\ \end{bmatrix} y_{t|t-1} </math>
where:
1) <math> \hat{\textbf{x}}_{t|t-1} </math> is estimated via a standard Kalman filter;
2) <math> y_{t|t-1} = z(t) - \hat{\textbf{x}}_{t|t-1} </math> is the innovation produced considering the estimate of the standard Kalman filter;
3) the various <math> \hat{\textbf{x}}_{t-i|t} </math> with <math> i = 0,\ldots,N </math> are new variables, i.e. they do not appear in the standard Kalman filter;
4) the gains are computed via the following scheme:
<math> K^{(i)} = P^{(i)} H^{T} \left[ H P H^{T} + R \right]^{-1} </math>
and
<math> P^{(i)} = P \left[ \left[ F - K H \right]^{T} \right]^{i} </math>
where <math> P </math> and <math> K </math> are the prediction error covariance and the gains of the standard Kalman filter.
Note that if we define the estimation error covariance
<math> P_{i} := E \left[ \left( \textbf{x}_{t-i} - \hat{\textbf{x}}_{t-i|t} \right)^{*} \left( \textbf{x}_{t-i} - \hat{\textbf{x}}_{t-i|t} \right) | z_{1} \ldots z_{t} \right] </math>
then we have that the improvement on the estimation of <math> \textbf{x}_{t-i} </math> is given by:
<math> P - P_{i} = \sum_{j = 0}^{i} \left[ P^{(j)} H^{T} \left[ H P H^{T} + R \right]^{-1} H \left( P^{(i)} \right)^{T} \right] </math>
Fixed-interval filters
The optimal fixed-interval smoother provides the optimal estimate of <math>\hat{\textbf{x}}_{k | n}</math> (<math>k \leq n</math>) using the measurements from a fixed interval <math>\textbf{z}_{1}</math> to <math>\textbf{z}_{n}</math>. This is also called Kalman Smoothing.
There exists an efficient two-pass algorithm, Rauch-Tung-Striebel Algorithm, for achieving this. The main equations of the smoother is the following (assuming <math>\textbf{B}_{k} = \textbf{0}</math>):
- forward pass: regular Kalman filter algorithm
- backward pass: <math> \hat{\textbf{x}}_{k|n} = \tilde{F}_k \hat{\textbf{x}}_{k+1|n} + \tilde{K}_k \hat{\textbf{x}}_{k+1|k} </math>, where
- <math> \tilde{\textbf{F}}_k = \textbf{F}_k^{-1} (\textbf{I} - \textbf{Q}_k \textbf{P}_{k+1|k}^{-1}) </math>
- <math> \tilde{\textbf{K}}_k = \textbf{F}_k^{-1} \textbf{Q}_k \textbf{P}_{k+1|k}^{-1} </math>
Нелинейные фильтры
Изначально фильтр Калмана ограничен по области применения линейными системами. Однако большинство интересных для анализа систем являются нелинейными. Эта нелинейность может иметь отношение к модели процесса, к модели наблюдения или к обоим.
Source(s): Фильтр Калмана
Расширенный фильтр Калмана (EKF)
В расширенном фильтре Калмана, (extended Kalman filter, EKF) не требуется, чтобы модель состояния системы и модель наблюдения были линейными функциями, вместо этого требуется, чтобы они были дифференцируемы по состоянию системы.
- <math>\textbf{x}_{k} = f(\textbf{x}_{k-1}, \textbf{u}_{k}) + \textbf{w}_{k}</math>
- <math>\textbf{z}_{k} = h(\textbf{x}_{k}) + \textbf{v}_{k}</math>
В этой модели функция f используется для расчета предсказываемого оценочного состояния системы из предыдущего и аналогично функция h используется для предсказываемого результата измерения из предсказанного состояния системы. Не смотря на то, что f и h не могут быть применены для расчета ковариаций напрямую, мы можем использовать вместо них соответствующие матрицы частных производных (Якобианы) в соответствующих точках (в предыдущем и предсказанном состояниях системы).
На каждом шаге мы расчитываем эти Якобианы и просто подставляем их вместо матриц F и H в обычные формулы фильтра Калмана. Таким образом мы просто линеаризуем нелинейные функции f и h вблизи соответствующих точек, что допускается, т.к. они по объявленным в начале требованиям дифференцируемы.
Source(s): Фильтр Калмана
Сигма-точечный фильтр (UKF)
Когда модели состояния системы и наблюдения, а значит и функции предсказания состояния системы и модели наблюдения <math>f</math> и <math>h</math> (см. выше) – в значительной степени нелинейны, расширенная версия фильтра Калмана может быть не эффективна.[2] This is because the mean and covariance are propagated through linearization of the underlying non-linear model. The unscented Kalman filter (UKF) [2] uses a deterministic sampling technique known as the unscented transform to pick a minimal set of sample points (called sigma points) around the mean. These sigma points are then propagated through the non-linear functions, from which the mean and covariance of the estimate are then recovered. The result is a filter which more accurately captures the true mean and covariance. (This can be verified using Monte Carlo sampling or through a Taylor series expansion of the posterior statistics.) In addition, this technique removes the requirement to explicitly calculate Jacobians, which for complex functions can be a difficult task in itself (i.e., requiring complicated derivatives if done analytically or being computationally costly if done numerically).
Предсказание
As with the EKF, the UKF prediction can be used independently from the UKF update, in combination with a linear (or indeed EKF) update, or vice versa.
The estimated state and covariance are augmented with the mean and covariance of the process noise.
- <math> \textbf{x}_{k-1|k-1}^{a} = [ \hat{\textbf{x}}_{k-1|k-1}^{T} \quad E[\textbf{w}_{k}^{T}] \ ]^{T} </math>
- <math> \textbf{P}_{k-1|k-1}^{a} = \begin{bmatrix} & \textbf{P}_{k-1|k-1} & & 0 & \\ & 0 & &\textbf{Q}_{k} & \end{bmatrix} </math>
A set of 2L+1 sigma points is derived from the augmented state and covariance where L is the dimension of the augmented state.
k-1}^{0} </math> k-1}^{a} </math> k-1}^{i} </math> k-1}^{a} + \left ( \sqrt{ (L + \lambda) \textbf{P}_{k-1|k-1}^{a} } \right )_{i}</math> <math>i = 1..L \,\!</math> k-1}^{i} </math> k-1}^{a} - \left ( \sqrt{ (L + \lambda) \textbf{P}_{k-1|k-1}^{a} } \right )_{i-L}</math> <math>i = L+1,\dots{}2L \,\!</math>
где
k-1}^{a} } \right )_{i}</math>
это i-я колонка квадратного корня матрицы
k-1}^{a}</math>
использующего определение: квадратный корень A матрицы B удовлетворяет условию
<math>B \equiv A A^T</math>.
Квадратный корень матрицы должен рассчитываться используя устойчивые эффективные числовые методы, такие как Cholesky decomposition.
The sigma points are propagated through the transition function f.
- <math>\chi_{k|k-1}^{i} = f(\chi_{k-1|k-1}^{i}) \quad i = 0..2L </math>
The weighted sigma points are recombined to produce the predicted state and covariance.
- <math>\hat{\textbf{x}}_{k|k-1} = \sum_{i=0}^{2L} W_{s}^{i} \chi_{k|k-1}^{i} </math>
- <math>\textbf{P}_{k|k-1} = \sum_{i=0}^{2L} W_{c}^{i}\ [\chi_{k|k-1}^{i} - \hat{\textbf{x}}_{k|k-1}] [\chi_{k|k-1}^{i} - \hat{\textbf{x}}_{k|k-1}]^{T} </math>
where the weights for the state and covariance are given by:
- <math>W_{s}^{0} = \frac{\lambda}{L+\lambda}</math>
- <math>W_{c}^{0} = \frac{\lambda}{L+\lambda} + (1 - \alpha^2 + \beta)</math>
- <math>W_{s}^{i} = W_{c}^{i} = \frac{1}{2(L+\lambda)}</math>
- <math>\lambda = \alpha^2 (L+\kappa) - L \,\! </math>
Typical values for <math>\alpha</math>, <math>\beta</math>, and <math>\kappa</math> are <math>10^{-3}</math>, 2 and 0 respectively. (These values should suffice for most purposes.)Шаблон:Fact
Учет наблюдений
The predicted state and covariance are augmented as before, except now with the mean and covariance of the measurement noise.
- <math> \textbf{x}_{k|k-1}^{a} = [ \hat{\textbf{x}}_{k|k-1}^{T} \quad E[\textbf{v}_{k}^{T}] \ ]^{T} </math>
- <math> \textbf{P}_{k|k-1}^{a} = \begin{bmatrix} & \textbf{P}_{k|k-1} & & 0 & \\ & 0 & &\textbf{R}_{k} & \end{bmatrix} </math>
As before, a set of 2L + 1 sigma points is derived from the augmented state and covariance where L is the dimension of the augmented state.
k-1}^{0} </math> k-1}^{a} </math> k-1}^{i} </math> k-1}^{a} + \left ( \sqrt{ (L + \lambda) \textbf{P}_{k|k-1}^{a} } \right )_{i}</math> <math>i = 1..L \,\!</math> k-1}^{i} </math> k-1}^{a} - \left ( \sqrt{ (L + \lambda) \textbf{P}_{k|k-1}^{a} } \right )_{i-L}</math> <math>i = L+1,\dots{}2L \,\!</math>
Alternatively if the UKF prediction has been used the sigma points themselves can be augmented along the following lines
- <math> \chi_{k|k-1} := [ \chi_{k|k-1}^T \quad E[\textbf{v}_{k}^{T}] \ ]^{T} \pm \sqrt{ (L + \lambda) \textbf{R}_{k}^{a} }</math>
где
- <math> \textbf{R}_{k}^{a} = \begin{bmatrix} & 0 & & 0 & \\ & 0 & &\textbf{R}_{k} & \end{bmatrix} </math>
The sigma points are projected through the observation function h.
- <math>\gamma_{k}^{i} = h(\chi_{k|k-1}^{i}) \quad i = 0..2L </math>
The weighted sigma points are recombined to produce the predicted measurement and predicted measurement covariance.
- <math>\hat{\textbf{z}}_{k} = \sum_{i=0}^{2L} W_{s}^{i} \gamma_{k}^{i} </math>
- <math>\textbf{P}_{z_{k}z_{k}} = \sum_{i=0}^{2L} W_{c}^{i}\ [\gamma_{k}^{i} - \hat{\textbf{z}}_{k}] [\gamma_{k}^{i} - \hat{\textbf{z}}_{k}]^{T} </math>
The state-measurement cross-covariance matrix,
- <math>\textbf{P}_{x_{k}z_{k}} = \sum_{i=0}^{2L} W_{c}^{i}\ [\chi_{k|k-1}^{i} - \hat{\textbf{x}}_{k|k-1}] [\gamma_{k}^{i} - \hat{\textbf{z}}_{k}]^{T} </math>
is used to compute the UKF Kalman gain.
- <math>K_{k} = \textbf{P}_{x_{k}z_{k}} \textbf{P}_{z_{k}z_{k}}^{-1}</math>
As with the Kalman filter, the updated state is the predicted state plus the innovation weighted by the Kalman gain,
- <math>\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}_{k|k-1} + K_{k}( \textbf{z}_{k} - \hat{\textbf{z}}_{k} )</math>
And the updated covariance is the predicted covariance, minus the predicted measurement covariance, weighted by the Kalman gain.
- <math>\textbf{P}_{k|k} = \textbf{P}_{k|k-1} - K_{k} \textbf{P}_{z_{k}z_{k}} K_{k}^{T} </math>
Source(s): Фильтр Калмана
Фильтр Калмана-Бьюси
Фильтр Калмана-Бьюси это непрерывная версия фильтра Калмана .[3][4]
Он основан на следующей модели пространства состояний системы
- <math>\frac{d}{dt}\mathbf{x}(t) = \mathbf{F}(t)\mathbf{x}(t) + \mathbf{w}(t)</math>
- <math>\mathbf{z}(t) = \mathbf{H}(t) \mathbf{x}(t) + \mathbf{v}(t)</math>
где матрицами ковариаций погрешностей <math>\mathbf{w}(t)</math> и <math>\mathbf{v}(t)</math> являются <math>\mathbf{Q}(t)</math> и <math>\mathbf{R}(t)</math>, соответственно.
Фильтр состоит из двух дифференциальных уравнений, одно для функции оценочного состояния системы, а второе для функции матрицы ковариаций этого состояния:
- <math>\frac{d}{dt}\hat{\mathbf{x}}(t) = \mathbf{F}(t)\hat{\mathbf{x}}(t) + \mathbf{K}(t) (\mathbf{z}(t)-\mathbf{H}(t)\hat{\mathbf{x}}(t))</math>
- <math>\frac{d}{dt}\mathbf{P}(t) = \mathbf{F}(t)\mathbf{P}(t) + \mathbf{P}(t)\mathbf{F}^{T}(t) + \mathbf{Q}(t) - \mathbf{K}(t)\mathbf{R}(t)\mathbf{K}^{T}(t)</math>
где коэффициент усиления Калмана определен, как
- <math>\mathbf{K}(t)=\mathbf{P}(t)\mathbf{H}^{T}(t)\mathbf{R}^{-1}(t)</math>
Обратите внимение, что в выражении для <math>\mathbf{K}(t)</math> матрица ковариаций погрешности наблюдения <math>\mathbf{R}(t)</math> является одновременно матрицей ковариаций ошибки корректировки вектора состояния системы <math>\tilde{\mathbf{y}}(t)=\mathbf{z}(t)-\mathbf{H}(t)\hat{\mathbf{x}}(t)</math>; эти ковариации совпадают только в непрерывном случае.[5]
В непрерывном случае отсутствуют отдельные шаги для расчета результата управляющего воздействия и внесения информации о результатах наблюдений, которые можно выделить для дискретной по времени модели.
Второе дифференциальное уравнение для ковариаций является примером уравнения Риккати.
Source(s): Фильтр Калмана
Сноски
- ↑ Roweis, S. and Ghahramani, Z., A unifying review of linear Gaussian models, Neural Comput. Vol. 11, No. 2, (February 1999), pp. 305-345.
- ↑ 1 2 Шаблон:Cite journal
- ↑ Bucy, R.S. and Joseph, P.D., Filtering for Stochastic Processes with Applications to Guidance, John Wiley & Sons, 1968; 2nd Edition, AMS Chelsea Publ., 2005. ISBN 0821837826
- ↑ Jazwinski, Andrew H., Stochastic processes and filtering theory, Academic Press, New York, 1970. ISBN 0123815509
- ↑ Kailath, Thomas, "An innovation approach to least-squares estimation Part I: Linear filtering in additive white noise", IEEE Transactions on Automatic Control, 13(6), 646-655, 1968