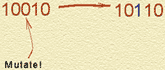Генетические алгоритмы — различия между версиями
Digit (обсуждение | вклад) (→'''Генетические алгоритмы: почему они работают? когда их применять?''') |
Ruslan (обсуждение | вклад) (→Ссылки) |
||
| (не показаны 53 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{CopyRightBlock|Публикуется с некоторыми изменениями.<br /> | |
| + | взято отсюда:<br /> | ||
| + | http://www.mnogosmenka.ru/drugoe/genetitiskie.htm<br /> | ||
| + | © '''РОСС КЛЕМЕНТ''', Опубликовано: 16.3.1999}} | ||
| + | [[Category:Справочник решений|{{PAGENAME}}]] | ||
| − | ''' | + | '''Генетические алгоритмы (ГА): почему и как они работают? когда их применять?''' |
| + | __TOC__ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''XIX веке Чарльз Дарвин совершил кругосветное плавание, собирая информацию для теории эволюции на основе естественного отбора, при котором выживает сильнейший. Мог ли он предполагать, что сто лет спустя математики будут использовать эту теорию для решения задачи об оптимальном маршруте кругосветного путешествия с остановками на многих маленьких островах?..'' | ''XIX веке Чарльз Дарвин совершил кругосветное плавание, собирая информацию для теории эволюции на основе естественного отбора, при котором выживает сильнейший. Мог ли он предполагать, что сто лет спустя математики будут использовать эту теорию для решения задачи об оптимальном маршруте кругосветного путешествия с остановками на многих маленьких островах?..'' | ||
''Росс Клемент (Ross Clement; R.P.Clement@westminster.ac.uk) окончил Оклендский университет (Новая Зеландия) по специальности "Компьютерные науки". Защитил диссертацию и получил степень "Doctor of Engineering" в Техническом университете Тойохаши (Toyohashi University of Technology) в Японии. В 1991-93 годах занимался приложениями генетических алгоритмов к задачам составления расписаний. С 1993 года - лектор в Школе компьютерных наук в Харроу, в Университете Вестминстера (Лондон). Научные интересы: генетические алгоритмы, интеллектуальные агенты, фрактальная музыка.'' | ''Росс Клемент (Ross Clement; R.P.Clement@westminster.ac.uk) окончил Оклендский университет (Новая Зеландия) по специальности "Компьютерные науки". Защитил диссертацию и получил степень "Doctor of Engineering" в Техническом университете Тойохаши (Toyohashi University of Technology) в Японии. В 1991-93 годах занимался приложениями генетических алгоритмов к задачам составления расписаний. С 1993 года - лектор в Школе компьютерных наук в Харроу, в Университете Вестминстера (Лондон). Научные интересы: генетические алгоритмы, интеллектуальные агенты, фрактальная музыка.'' | ||
| − | + | == Что такое ГА и как они могут применяться? == | |
| + | |||
| + | [[Изображение:20-1.gif|thumb|Рис.1 - Эффективный и неэффективный маршруты в задаче коммивояжера (ЗКВ).]] | ||
Круг практических задач, решаемых компьютерами, постоянно расширяется. Компьютер может составить расписание деловых встреч, удобный график работы сменных экипажей автобусов, научить вас играть на пианино, а иногда и заставить задуматься, способны ли вы вообще научиться игре в шахматы. Однако это возможно лишь при одном маленьком, но неприятном условии: какой-то несчастный должен написать программу, которая будет все это делать. Как жаль, что мы не можем просто перечислить, что хотелось бы получить от программы, а все скучные детали того, как именно она это сделает, предоставить самой машине! Генетические алгоритмы, конечно, не претендуют на роль эдакого "святого Грааля" в сфере программирования, но в ряде приложений они способны на нечто довольно близкое.<br /> | Круг практических задач, решаемых компьютерами, постоянно расширяется. Компьютер может составить расписание деловых встреч, удобный график работы сменных экипажей автобусов, научить вас играть на пианино, а иногда и заставить задуматься, способны ли вы вообще научиться игре в шахматы. Однако это возможно лишь при одном маленьком, но неприятном условии: какой-то несчастный должен написать программу, которая будет все это делать. Как жаль, что мы не можем просто перечислить, что хотелось бы получить от программы, а все скучные детали того, как именно она это сделает, предоставить самой машине! Генетические алгоритмы, конечно, не претендуют на роль эдакого "святого Грааля" в сфере программирования, но в ряде приложений они способны на нечто довольно близкое.<br /> | ||
| Строка 26: | Строка 26: | ||
- и, в конечном счете, умирают.<br /> | - и, в конечном счете, умирают.<br /> | ||
| − | + | == Схема работы генетического алгоритма. == | |
| + | |||
| + | [[Изображение:20-2.gif|thumb|Рис.2 - Схема работы генетического алгоритма.]] | ||
Схема типичного генетического алгоритма представлена на рис. 2. В статье мы обсудим, как работают различные блоки из этой схемы. | Схема типичного генетического алгоритма представлена на рис. 2. В статье мы обсудим, как работают различные блоки из этой схемы. | ||
| + | |||
| + | |||
| + | === Хромосомы === | ||
Разработка генетического алгоритма начинается с конструирования двоичной хромосомы, представляющей возможные решения этой задачи. Традиционно генетические алгоритмы используют для этого двоичные строки фиксированной длины. Например, для нашей ЗКВ с четырьмя городами, которые надо поочередно посетить, проще всего было бы выделить по 2 бита на каждый город, получив 8-битовую хромосому. Рисунок 3 поясняет, как записывается информация на такую хромосому. Можно построить множество случайных строк из 8 бит, интерпретируя их как маршруты объезда городов. | Разработка генетического алгоритма начинается с конструирования двоичной хромосомы, представляющей возможные решения этой задачи. Традиционно генетические алгоритмы используют для этого двоичные строки фиксированной длины. Например, для нашей ЗКВ с четырьмя городами, которые надо поочередно посетить, проще всего было бы выделить по 2 бита на каждый город, получив 8-битовую хромосому. Рисунок 3 поясняет, как записывается информация на такую хромосому. Можно построить множество случайных строк из 8 бит, интерпретируя их как маршруты объезда городов. | ||
| + | <br /> | ||
Табл. 1. Случайно выбранные хромосомы. | Табл. 1. Случайно выбранные хромосомы. | ||
| Строка 54: | Строка 60: | ||
Но эта хромосома слишком проста для ЗКВ любого размера. Один из ее недостатков заключается в том, что большинство двоичных строк из 8 бит не соответствуют допустимым маршрутам. Как видно из таблицы 1, мы можем получить маршруты, проходящие через некоторые города дважды, а через другие - ни разу. Можно было бы рассматривать и такие "не-решения", с тем чтобы настоящие решения вытеснили их в процессе эволюции, но в дальнейшем мы увидим, что это неэффективный путь. Лучше придумать другую кодировку, чтобы любая двоичная строка представляла допустимый (но, конечно, не всегда разумный) маршрут в ЗКВ. | Но эта хромосома слишком проста для ЗКВ любого размера. Один из ее недостатков заключается в том, что большинство двоичных строк из 8 бит не соответствуют допустимым маршрутам. Как видно из таблицы 1, мы можем получить маршруты, проходящие через некоторые города дважды, а через другие - ни разу. Можно было бы рассматривать и такие "не-решения", с тем чтобы настоящие решения вытеснили их в процессе эволюции, но в дальнейшем мы увидим, что это неэффективный путь. Лучше придумать другую кодировку, чтобы любая двоичная строка представляла допустимый (но, конечно, не всегда разумный) маршрут в ЗКВ. | ||
| − | Табл. | + | <br /> |
| + | Табл. 2. Случайно выбранные 5-битовые хромосомы. | ||
{| class="wikitable" | {| class="wikitable" | ||
| Строка 75: | Строка 82: | ||
Вот одна из таких кодировок: первые два бита - номер первого города в маршруте, вторые два бита - номер того из оставшихся трех городов, который посещается вторым, пятый бит определяет выбор из оставшихся двух городов, а на номер последнего, четвертого города битов выделять не нужно. Мы получаем 5-битовую хромосому. В таблице 2 показаны несколько таких хромосом и соответствующих им маршрутов. Заметим, что и здесь возникает небольшая проблема, так как вторые два бита могут представлять четыре различных числа, которые надо сопоставить трем различным городам. С этим можно справиться, решив, что и 11, и 00 соответствуют первому из этих трех городов. Не очень удачное решение, так как оно вдвое повышает шансы наугад выбрать именно этот город, но пока это нам не очень мешает. | Вот одна из таких кодировок: первые два бита - номер первого города в маршруте, вторые два бита - номер того из оставшихся трех городов, который посещается вторым, пятый бит определяет выбор из оставшихся двух городов, а на номер последнего, четвертого города битов выделять не нужно. Мы получаем 5-битовую хромосому. В таблице 2 показаны несколько таких хромосом и соответствующих им маршрутов. Заметим, что и здесь возникает небольшая проблема, так как вторые два бита могут представлять четыре различных числа, которые надо сопоставить трем различным городам. С этим можно справиться, решив, что и 11, и 00 соответствуют первому из этих трех городов. Не очень удачное решение, так как оно вдвое повышает шансы наугад выбрать именно этот город, но пока это нам не очень мешает. | ||
| + | |||
| + | === Выживание сильнейших === | ||
Сконструировав хромосому, мы без всякого труда можем построить 500 случайно выбранных маршрутов в нашей ЗКВ, сгенерировав 500 случайных 5-битовых чисел. Но ведь мы как раз и мечтали свести программирование к минимуму при решении трудных задач. Значит, цель достигнута? Разумеется, это зависит от того, насколько хороши полученные таким путем решения. Другими словами, затратит ли наш коммивояжер минимально возможное время на свои переезды из города в город, если воспользуется некоторыми из предлагаемых маршрутов? | Сконструировав хромосому, мы без всякого труда можем построить 500 случайно выбранных маршрутов в нашей ЗКВ, сгенерировав 500 случайных 5-битовых чисел. Но ведь мы как раз и мечтали свести программирование к минимуму при решении трудных задач. Значит, цель достигнута? Разумеется, это зависит от того, насколько хороши полученные таким путем решения. Другими словами, затратит ли наш коммивояжер минимально возможное время на свои переезды из города в город, если воспользуется некоторыми из предлагаемых маршрутов? | ||
| Строка 84: | Строка 93: | ||
Реализация генетического алгоритма предполагает задание функции приспособленности, или фитнес-функции (fitness function). Эта функция получает на вход двоичную хромосому и возвращает число, показывающее, насколько хороша эта хромосома. В реализованном автором генетическом алгоритме решения ЗКВ сначала определяется наихудшая хромосома (отвечающая самому длинному из маршрутов) и измеряется длина этого маршрута (в километрах). Полученное число умножается на 1,1 и объявляется плохой длиной, по отношению к которой оценивается качество остальных хромосом: приспособленность хромосомы вычисляется как разность между плохой длиной и длиной маршрута, заданного данной хромосомой. В результате этих несколько запутанных вычислений каждой хромосоме ставится в соответствие ее приспособленность (fitness) - число, которое оказывается сравнительно маленьким для плохих (длинных) маршрутов и сравнительно большим для хороших (коротких) маршрутов. | Реализация генетического алгоритма предполагает задание функции приспособленности, или фитнес-функции (fitness function). Эта функция получает на вход двоичную хромосому и возвращает число, показывающее, насколько хороша эта хромосома. В реализованном автором генетическом алгоритме решения ЗКВ сначала определяется наихудшая хромосома (отвечающая самому длинному из маршрутов) и измеряется длина этого маршрута (в километрах). Полученное число умножается на 1,1 и объявляется плохой длиной, по отношению к которой оценивается качество остальных хромосом: приспособленность хромосомы вычисляется как разность между плохой длиной и длиной маршрута, заданного данной хромосомой. В результате этих несколько запутанных вычислений каждой хромосоме ставится в соответствие ее приспособленность (fitness) - число, которое оказывается сравнительно маленьким для плохих (длинных) маршрутов и сравнительно большим для хороших (коротких) маршрутов. | ||
| − | + | [[Изображение:20-3.gif|thumb|Рис.3 - Декодирование двоичной хромосомы.]] | |
Вернемся к "выживанию сильнейших". Будем использовать "колесо рулетки" для того, чтобы выбрать из текущего поколения хромосомы, которые сохранятся в следующем поколении. Если читатель представляет себе обычную рулетку, он согласится, что у шарика одинаковые шансы остановиться в любом из секторов. Но если рулетка разделена на неравные секторы (рис. 4), вероятность того, что шарик остановится в широком секторе, велика, а в узком - мала. Предположим, что каждый сектор нашей "кривой" рулетки отвечает одной из хромосом, а ширина сектора пропорциональна ее качеству. Запустив рулетку 500 раз, мы получим новое поколение хромосом. | Вернемся к "выживанию сильнейших". Будем использовать "колесо рулетки" для того, чтобы выбрать из текущего поколения хромосомы, которые сохранятся в следующем поколении. Если читатель представляет себе обычную рулетку, он согласится, что у шарика одинаковые шансы остановиться в любом из секторов. Но если рулетка разделена на неравные секторы (рис. 4), вероятность того, что шарик остановится в широком секторе, велика, а в узком - мала. Предположим, что каждый сектор нашей "кривой" рулетки отвечает одной из хромосом, а ширина сектора пропорциональна ее качеству. Запустив рулетку 500 раз, мы получим новое поколение хромосом. | ||
| − | + | [[Изображение:20-4.gif|thumb|Рис.4 - Выбор при помощи колеса рулетки.]] | |
Так как рулетка "кривая", вполне возможно, что некоторые из хромосом данного поколения будут выбраны несколько раз, а некоторые - ни разу. Хотя случайный характер выбора и может привести к отсеву ("смерти") очень хорошо приспособленных хромосом и увеличению количества плохо приспособленных хромосом, в среднем число хороших хромосом будет расти, а плохих - уменьшаться. Можно ожидать, что качество следующей популяции будет, в среднем, выше качества предыдущей. Начинают работать факторы эволюции, так как хромосомы фактически вынуждены бороться за место в следующем поколении под действием "искусственного дефицита" (artificial scarcity). | Так как рулетка "кривая", вполне возможно, что некоторые из хромосом данного поколения будут выбраны несколько раз, а некоторые - ни разу. Хотя случайный характер выбора и может привести к отсеву ("смерти") очень хорошо приспособленных хромосом и увеличению количества плохо приспособленных хромосом, в среднем число хороших хромосом будет расти, а плохих - уменьшаться. Можно ожидать, что качество следующей популяции будет, в среднем, выше качества предыдущей. Начинают работать факторы эволюции, так как хромосомы фактически вынуждены бороться за место в следующем поколении под действием "искусственного дефицита" (artificial scarcity). | ||
| + | |||
| + | === Кроссинговер (crossover): по-нашему - скрещивание === | ||
Однако здесь возникает вопрос: получили ли мы лучшие решения, чем те, что были в предыдущем поколении? Короткий ответ: нет, не получили. Колесо рулетки не создает новых решений. Первое, что нужно для создания таких решений, - кроссинговер (crossover). | Однако здесь возникает вопрос: получили ли мы лучшие решения, чем те, что были в предыдущем поколении? Короткий ответ: нет, не получили. Колесо рулетки не создает новых решений. Первое, что нужно для создания таких решений, - кроссинговер (crossover). | ||
| − | + | [[Изображение:20-5.gif|thumb|Рис.5 - Пример кроссинговера.]] | |
При кроссинговере хромосомы группируются в пары, и случайным образом выбирается точка кроссинговера. Например, для наших 5-битовых хромосом мы можем наугад выбрать одну из точек 1, 2, 3, 4. Операция кроссинговера состоит в следующем: мы меняем местами участки выбранных хромосом слева от точки кроссинговера. Это показано на рис. 5 для точки кроссинговера 3. | При кроссинговере хромосомы группируются в пары, и случайным образом выбирается точка кроссинговера. Например, для наших 5-битовых хромосом мы можем наугад выбрать одну из точек 1, 2, 3, 4. Операция кроссинговера состоит в следующем: мы меняем местами участки выбранных хромосом слева от точки кроссинговера. Это показано на рис. 5 для точки кроссинговера 3. | ||
| Строка 101: | Строка 112: | ||
Не все пары хромосом в новой популяции подвергаются кроссинговеру. Некоторые хромосомы остаются неизменными. Это зависит от того, какой стороной упадет виртуальная монетка, которую подбрасывают для каждой пары. Если выпадает орел (это может происходить с некоторой фиксированной вероятностью - например, 0,1 или 0,3, или 0,6 и т. д.), то происходит кроссинговер со случайно выбранной точкой. | Не все пары хромосом в новой популяции подвергаются кроссинговеру. Некоторые хромосомы остаются неизменными. Это зависит от того, какой стороной упадет виртуальная монетка, которую подбрасывают для каждой пары. Если выпадает орел (это может происходить с некоторой фиксированной вероятностью - например, 0,1 или 0,3, или 0,6 и т. д.), то происходит кроссинговер со случайно выбранной точкой. | ||
| − | + | === Мутации === | |
| + | |||
| + | [[Изображение:20-6.gif|thumb|Рис.6 - Пример мутации.]] | ||
Последний этап - мутация (mutation). Даже для больших популяций может оказаться, что не все биты генетического материала в ней представлены. Например, если первый бит у всех хромосом равен 0, то кроссинговер никогда не породит решение с 1 в первом бите. Мутация предназначена для того, чтобы избежать таких ситуаций и увеличить вариабельность популяции. Частота мутации обычно очень низкая - отвечающая за нее виртуальная монетка должна падать орлом вверх один раз за сто или тысячу бросаний. Если выпадает орел, в хромосоме выбирается случайный бит и его значение меняется на противоположное (0 превращается в 1, а 1 - в 0). На рис. 6 показан процесс мутации одной из хромосом. | Последний этап - мутация (mutation). Даже для больших популяций может оказаться, что не все биты генетического материала в ней представлены. Например, если первый бит у всех хромосом равен 0, то кроссинговер никогда не породит решение с 1 в первом бите. Мутация предназначена для того, чтобы избежать таких ситуаций и увеличить вариабельность популяции. Частота мутации обычно очень низкая - отвечающая за нее виртуальная монетка должна падать орлом вверх один раз за сто или тысячу бросаний. Если выпадает орел, в хромосоме выбирается случайный бит и его значение меняется на противоположное (0 превращается в 1, а 1 - в 0). На рис. 6 показан процесс мутации одной из хромосом. | ||
| + | |||
| + | |||
| + | == Процесс поиска решений == | ||
Мутация и кроссинговер могут порождать новые решения, которые никогда не встречались в предыдущих поколениях. Для оценки качества этих решений вычисляется фитнес-функция. На этом построение нового поколения решений заканчивается. | Мутация и кроссинговер могут порождать новые решения, которые никогда не встречались в предыдущих поколениях. Для оценки качества этих решений вычисляется фитнес-функция. На этом построение нового поколения решений заканчивается. | ||
| Строка 109: | Строка 125: | ||
При переходе от первого поколения ко второму может появиться решение более высокого качества. Однако и оно, скорее всего, еще не будет приемлемым. Как и в естественной эволюции, одна смена поколений не приводит к заметному прогрессу вида (в нашем случае - набора решений ЗКВ). Поэтому генетический алгоритм создает следующее поколение, последовательно применяя "выживание сильнейшего", кроссинговер и мутацию. Затем таким же образом обрабатывается это новое поколение и так далее. Процесс повторяется тысячи или даже миллионы раз. При этом могут постепенно "выводиться" очень хорошие маршруты путешествия коммивояжера, расписания работы автобусных смен, решения других задач. | При переходе от первого поколения ко второму может появиться решение более высокого качества. Однако и оно, скорее всего, еще не будет приемлемым. Как и в естественной эволюции, одна смена поколений не приводит к заметному прогрессу вида (в нашем случае - набора решений ЗКВ). Поэтому генетический алгоритм создает следующее поколение, последовательно применяя "выживание сильнейшего", кроссинговер и мутацию. Затем таким же образом обрабатывается это новое поколение и так далее. Процесс повторяется тысячи или даже миллионы раз. При этом могут постепенно "выводиться" очень хорошие маршруты путешествия коммивояжера, расписания работы автобусных смен, решения других задач. | ||
| − | Замечательная черта генетических алгоритмов состоит в том, что они выполняют множество изощренных манипуляций с решениями задачи, но без малейшего представления о том, что же при этом | + | Замечательная черта генетических алгоритмов состоит в том, что они выполняют множество изощренных манипуляций с решениями задачи, но без малейшего представления о том, что же при этом происходит! Процедура кроссинговера берет два решения ЗКВ и создает из них два новых решения, смешивая части первого и второго. Все, что для этого нужно, - выбор случайной позиции в битовой строке и перестановка двух подстрок. Та же самая процедура, что манипулирует с решениями ЗКВ, может помочь наилучшим образом рассадить гостей за свадебным столом. Единственное, что нужно знать, - длину двоичной хромосомы. То же самое относится и к процедурам мутации, выживания сильнейшего и даже создания начальной популяции. Благодаря этому свойству достаточно один раз программно реализовать генетический алгоритм (а еще лучше - загрузить уже готовую программу из Интернета), а потом использовать его для решения множества самых разнообразных задач без сколько-нибудь серьезного изменения кода. |
| + | |||
Фитнес-функция - это единственная часть программы, которая должна понимать, что же на самом деле кодирует хромосома. Поэтому для каждого приложения надо писать новые фитнес-функции. К счастью, они обычно довольно просты, особенно по сравнению с программой, которая могла бы понадобиться для полного решения задачи. Очень трудно написать программу, дающую хотя бы просто "хорошие" решения больших ЗКВ. Очень легко написать функцию, которая вычисляет длину данного маршрута и вычитает ее из некоего опорного значения. Очень трудно написать программу, которая строит расписания работы экипажей для автобусных компаний. Очень легко написать процедуру, которая подсчитывает количество шоферов и оценивает те расписания, где заняты (читай: оплачиваются) меньше шоферов, выше, чем те, где шоферов нужно больше. Для ряда приложений генетические алгоритмы приближаются к мифической системе, о которой мы упоминали: "дай описание задачи и жди готового решения". | Фитнес-функция - это единственная часть программы, которая должна понимать, что же на самом деле кодирует хромосома. Поэтому для каждого приложения надо писать новые фитнес-функции. К счастью, они обычно довольно просты, особенно по сравнению с программой, которая могла бы понадобиться для полного решения задачи. Очень трудно написать программу, дающую хотя бы просто "хорошие" решения больших ЗКВ. Очень легко написать функцию, которая вычисляет длину данного маршрута и вычитает ее из некоего опорного значения. Очень трудно написать программу, которая строит расписания работы экипажей для автобусных компаний. Очень легко написать процедуру, которая подсчитывает количество шоферов и оценивает те расписания, где заняты (читай: оплачиваются) меньше шоферов, выше, чем те, где шоферов нужно больше. Для ряда приложений генетические алгоритмы приближаются к мифической системе, о которой мы упоминали: "дай описание задачи и жди готового решения". | ||
| − | + | == Сравнение ГА с другими методами решения задач == | |
| + | [[Изображение:20-7.gif|thumb|Рис.7 - Предсказуемая (а) и непредсказуемая (b) фитнес-функции.]] | ||
Для того чтобы понять, почему генетические алгоритмы работают, задумаемся над понятием пространства поиска. Пространство поиска - это множество возможных решений задачи. Например, это может быть множество всех возможных расстановок фигур на шахматной доске. Если мы нарисуем график приспособленности решений для простой задачи, мы можем получить как простое и предсказуемое (рис. 7a), так и более сложное (рис. 7b) пространство поиска. И в том, и в другом случае пространство поиска одномерно. Хромосома представляет одно число, которое и описывает решение (например, это может быть температура, при которой лучше всего растут помидоры). Размерность пространства поиска для более сложных задач может достигать нескольких сотен; в этом случае рисовать какие-либо графики невозможно, а программы поиска становятся крайне сложными. | Для того чтобы понять, почему генетические алгоритмы работают, задумаемся над понятием пространства поиска. Пространство поиска - это множество возможных решений задачи. Например, это может быть множество всех возможных расстановок фигур на шахматной доске. Если мы нарисуем график приспособленности решений для простой задачи, мы можем получить как простое и предсказуемое (рис. 7a), так и более сложное (рис. 7b) пространство поиска. И в том, и в другом случае пространство поиска одномерно. Хромосома представляет одно число, которое и описывает решение (например, это может быть температура, при которой лучше всего растут помидоры). Размерность пространства поиска для более сложных задач может достигать нескольких сотен; в этом случае рисовать какие-либо графики невозможно, а программы поиска становятся крайне сложными. | ||
| Строка 119: | Строка 137: | ||
Рассмотрим один из простых методов поиска - метод восхождения (hillclimbing). Он работает так: сначала генерируется случайное решение (например, маршрут в ЗКВ), затем в него вносится "единичное" возмущение (например, меняется местами пара городов), и возмущенное решение сравнивают с исходным. Если новый маршрут короче, он сохраняется, а старый отбрасывается. Если новый маршрут длиннее старого, то сохраняется старый. Затем процесс повторяется с сохраненным решением, но уже с другим единичным возмущением, и так далее. Если в течение, скажем, тысячи итераций решение не улучшается, оно объявляется оптимальным, и процесс останавливается. | Рассмотрим один из простых методов поиска - метод восхождения (hillclimbing). Он работает так: сначала генерируется случайное решение (например, маршрут в ЗКВ), затем в него вносится "единичное" возмущение (например, меняется местами пара городов), и возмущенное решение сравнивают с исходным. Если новый маршрут короче, он сохраняется, а старый отбрасывается. Если новый маршрут длиннее старого, то сохраняется старый. Затем процесс повторяется с сохраненным решением, но уже с другим единичным возмущением, и так далее. Если в течение, скажем, тысячи итераций решение не улучшается, оно объявляется оптимальным, и процесс останавливается. | ||
| − | + | [[Изображение:20-8.gif|thumb|Рис.8 - Нахождение оптимального решения (a) и локального максимума (b) методом восхождения.]] | |
При восхождении мы всегда идем вверх (в смысле функционала качества решения). Если пространство поиска простое и содержит лишь один пик приспособленности (рис. 8a), то при помощи восхождения мы найдем оптимальное решение. Если же оно более сложное и мы начинаем восхождение вблизи одного из небольших пиков (локальных максимумов), то глобальный оптимум вряд ли будет найден (рис. 8b). Для его нахождения надо пройти через область плохих решений. Метод восхождения на это не способен. | При восхождении мы всегда идем вверх (в смысле функционала качества решения). Если пространство поиска простое и содержит лишь один пик приспособленности (рис. 8a), то при помощи восхождения мы найдем оптимальное решение. Если же оно более сложное и мы начинаем восхождение вблизи одного из небольших пиков (локальных максимумов), то глобальный оптимум вряд ли будет найден (рис. 8b). Для его нахождения надо пройти через область плохих решений. Метод восхождения на это не способен. | ||
| − | + | [[Изображение:20-9.gif|thumb|Рис.9 - Генетический поиск.]] | |
| + | |||
| + | Генетический алгоритм действует более тонко. На рис. 9 мы видим, что генетическая популяция содержит много решений, разбросанных там и сям по пространству поиска. Мутация действует аналогично единичному возмущению в методе восхождения и приводит в основном к блужданию вблизи того пика, на котором находится решение. Однако операция кроссинговера порождает новые точки, которые могут попадать на удаленные пики, как показано на рис. 9. В этом отличие генетических алгоритмов от более простых, таких как восхождение. Генетический алгоритм эффективно просматривает пространство поиска, сохраняя хороших родителей, которые чаще, чем плохие, дают хорошее потомство. Поэтому такой алгоритм с большей вероятностью найдет хорошее решение задачи - например, симпатичный короткий маршрут в ЗКВ. | ||
| + | |||
| + | Теперь можно объяснить, почему мы не стали использовать первое, что пришло в голову, а именно 8-битовые хромосомы, допускавшие запрещенные решения, а сконструировали более сложные, 5-битовые. Было бы нетрудно построить фитнес-функцию, которая бы заведомо оценивала все допустимые решения выше, чем запрещенные. Генетический алгоритм мог бы тогда искать "наилучшие" решения, которые предположительно оказались бы допустимыми (то есть давали бы маршруты, проходящие через все города ровно по одному разу). Но плохо то, что размерность пространства поиска сильно возросла бы. Вместо 32 возможных решений для нашей ЗКВ с четырьмя городами нам пришлось бы рассматривать в 8 раз больше, то есть 256 возможных решений. А объем пространства поиска - важнейший, хотя и не единственный фактор, влияющий на качество работы генетического алгоритма. Большие пространства труднее "обыскать", и шансы найти оптимальное или просто хорошее решение уменьшаются. Конструкция хромосомы, уменьшающая объем пространства поиска, повышает эффективность генетического алгоритма. Для больших ЗКВ с сотнями городов наша наивная конструкция хромосомы неприемлема - алгоритм занимался бы только поиском допустимого решения, а до поиска хорошего решения дело бы вообще не дошло! Конструирование хромосомы обычно является самым важным этапом создания генетического алгоритма. | ||
| + | |||
| + | == Улучшение алгоритма - нестандартный кроссинговер == | ||
| + | |||
| + | Для работы с 5-битовой хромосомой необходимо чуть больше программирования, чем для работы с 8-битовой. За счет усложнения программы алгоритм можно улучшить и другим способом - применяя нестандартный кроссинговер. Метод "жадной генетики" (greedy genetics) вместо кроссинговера в случайной точке использует "жадный алгоритм" (greedy algorithm) для получения "хорошего" потомства. | ||
| + | |||
| + | Жадные алгоритмы применяются в самых разных задачах. Они являются, в сущности, реализацией в той или иной конкретной обстановке следующих абстрактных советов:<br /> | ||
| + | : - оцените все возможности улучшить данное решение; <br /> | ||
| + | : - выберите ту, при которой улучшение максимально; <br /> | ||
| + | : - используйте ее; <br /> | ||
| + | : - действуйте так до тех пор, пока не будет найдено приемлемое решение.<br /> | ||
| + | |||
| + | Жадное решение в применении к ЗКВ может выглядеть так.<br /> | ||
| + | : 1) Выберите произвольный город; он становится одновременно и начальным, и конечным пунктом маршрута.<br /> | ||
| + | : 2) Пока список городов не исчерпан, делайте следующее:<br /> | ||
| + | :: - Найдите город, ближайший либо к начальному, либо к конечному пункту. <br /> | ||
| + | :: - Добавьте новый город к новому маршруту: в конец, если он ближайший к конечному пункту, или в начало, если он ближайший к начальному пункту. | ||
| + | : 3) Запишите полученное решение.<br /> | ||
| + | |||
| + | Надежда получить очень хороший маршрут основана здесь на том, что на каждом шаге мы выбираем города, близкие друг к другу. Однако задачи типа ЗКВ часто оказываются слишком сложными для этого метода, а решения, найденные этим жадным алгоритмом, слишком плохими. | ||
| + | |||
| + | В жадной генетике на кроссинговер накладывается дополнительное условие: все сегменты (то есть отрезки маршрута, соединяющие два города) маршрутов-детей должны встречаться у одного из родителей. В результате качество детей обычно не уступает качеству родителей или превосходит его, и эволюция существенно ускоряется. Даррел Уайтли (Darrell Whitely) применил жадную генетику к ЗКВ и получил хорошие результаты [1]. Автор данной статьи использовал жадную генетику в задаче составления графиков работы сменных экипажей автобусов и тоже получил хорошие результаты [2]. Один из недостатков жадной генетики в том, что за счет ускорения эволюции алгоритм быстро находит приемлемое решение там, где обычный генетический алгоритм нашел бы лучшее решение, хотя и за более длительное время. В своих исследованиях я стремился вернуть как можно больше стохастики в процедуру кроссинговера, сохранив тот "рывок вперед", который дает жадная стратегия. Эксперименты убедили меня, что случайная составляющая совершенно необходима генетическим алгоритмам; без нее они работают гораздо хуже. | ||
| + | |||
| + | == Когда использовать ГА? == | ||
| + | |||
| + | И в заключение остановимся на том, когда же следует использовать генетические алгоритмы. В одних обстоятельствах они хороши, в других - не очень. В общем случае генетические алгоритмы не находят оптимального решения очень трудных задач. Если оптимальное решение задачи (например, ЗКВ с очень большим числом городов) не может быть найдено традиционными способами - например, методом сцепления ветвей (branch and bound method), - то и генетический алгоритм вряд ли найдет оптимум. С другой стороны, вполне возможно, что генетический алгоритм найдет достаточно хорошее решение. В конце концов, коммивояжеру в любом случае надо ехать продавать свои товары, даже если мы не уверены в абсолютной оптимальности маршрута! Но есть примеры, когда в очень трудных задачах, в том числе и в ЗКВ, с помощью генетических алгоритмов были получены очень хорошие решения. | ||
| + | |||
| + | В двух случаях генетические алгоритмы очень хороши. Первый случай: когда не известен способ точного решения задачи. Если мы знаем, как оценить приспособленность хромосом, то всегда можем заставить генетический алгоритм решать эту задачу. Второй случай: когда способ для точного решения существует, но он очень сложен в реализации, требует больших затрат времени и денег, то есть, попросту говоря, дело того не стоит. Пример - создание программы для составления персонального расписания на основе техники покрытия множеств с использованием линейного программирования. | ||
| + | |||
| + | Несмотря на то, что конструирование хромосом и фитнес-функций может потребовать значительных усилий, генетические алгоритмы легко реализуются даже с нуля и способны решать широкий круг задач. Используя аналогию с развитием живых организмов от простых форм к более сложным, генетические алгоритмы приблизились к тому, чтобы стать общим методом решения задач. Другие "природоподобные" парадигмы, такие как моделирование отжига (simulated annealing) и табу-поиск (taboo search), тоже позволяют решать аналогичные задачи. Но что может сравниться с чувством, которое вы испытываете, глядя на результат работы генетического алгоритма и невольно спрашивая себя: "Неужели все это могло образоваться лишь по воле случая?" | ||
| + | == Ссылки == | ||
| − | + | - Genetic Operators, the Fitness Landscape and the Traveling Salesman Problem, D.Whitley and K. Mathias, Parallel Problem Solving from Nature-PPSN 2. R. Mainner and B Manderick, eds., pp. 219-228. North Holland-Elsevier, 1992.<br /> | |
| + | - R.P.Clement & A.Wren, "Genetic Algorithms and Bus-Driver Scheduling".Presented at the 6th International Conference for Computer-Aided Transport Scheduling, Lisbon, Portugal, 1993.<br /> | ||
| + | http://www.ing.unlp.edu.ar/cetad/mos/TSPBIB_home.html - страница, посвященная ЗКВ (TSPBIB homepage). <br /> | ||
| + | http://www.aic.nrl.navy.mil/galist - архив генетических алгоритмов. <br /> | ||
| + | http://aif.wu-wien.ac.at/~geyers/archive/gpk/vuegpk.html - реализация генетического алгоритма на C++. <br /> | ||
| + | http://www4.ncsu.edu/eos/users/d/dhloughl/public/stable.htm - Java-апплет генетического алгоритма. <br /> | ||
| + | http://www.lalena.com/ai/tsp - генетический алгоритм для ЗКВ.<br /> | ||
| + | http://megaswf.com/serve/102223/ - визуальный пример пример работы генетического алгоритма <br /> | ||
| + | http://www.computerra.ru/offline/1999/289/2523/ - Эта статья была опубликована в журнале "Компьютерра" , 1999.<br /> | ||
Текущая версия на 14:22, 22 января 2011
| Авторские права. | |
Публикуется с некоторыми изменениями. взято отсюда: | |
Генетические алгоритмы (ГА): почему и как они работают? когда их применять?
Содержание
XIX веке Чарльз Дарвин совершил кругосветное плавание, собирая информацию для теории эволюции на основе естественного отбора, при котором выживает сильнейший. Мог ли он предполагать, что сто лет спустя математики будут использовать эту теорию для решения задачи об оптимальном маршруте кругосветного путешествия с остановками на многих маленьких островах?..
Росс Клемент (Ross Clement; R.P.Clement@westminster.ac.uk) окончил Оклендский университет (Новая Зеландия) по специальности "Компьютерные науки". Защитил диссертацию и получил степень "Doctor of Engineering" в Техническом университете Тойохаши (Toyohashi University of Technology) в Японии. В 1991-93 годах занимался приложениями генетических алгоритмов к задачам составления расписаний. С 1993 года - лектор в Школе компьютерных наук в Харроу, в Университете Вестминстера (Лондон). Научные интересы: генетические алгоритмы, интеллектуальные агенты, фрактальная музыка.
Что такое ГА и как они могут применяться?
Круг практических задач, решаемых компьютерами, постоянно расширяется. Компьютер может составить расписание деловых встреч, удобный график работы сменных экипажей автобусов, научить вас играть на пианино, а иногда и заставить задуматься, способны ли вы вообще научиться игре в шахматы. Однако это возможно лишь при одном маленьком, но неприятном условии: какой-то несчастный должен написать программу, которая будет все это делать. Как жаль, что мы не можем просто перечислить, что хотелось бы получить от программы, а все скучные детали того, как именно она это сделает, предоставить самой машине! Генетические алгоритмы, конечно, не претендуют на роль эдакого "святого Грааля" в сфере программирования, но в ряде приложений они способны на нечто довольно близкое.
Давайте для примера посмотрим, как можно использовать генетические алгоритмы для решения "задачи коммивояжера" (ЗКВ). ЗКВ состоит в том, чтобы по данному списку городов определить, в каком порядке коммивояжер должен посетить каждый из них по одному разу, чтобы получившийся маршрут был кратчайшим из возможных или хотя бы близким к таковому. На рис. 1 показаны два маршрута для одной задачи ЗКВ - эффективный и менее эффективный (то есть более длинный).
Генетические алгоритмы решают задачи, работая с популяцией из некоторого числа наугад взятых решений (обычно их несколько сотен; далее для определенности примем величину 500). При этом должны быть указаны правила, по которым решения, по аналогии с дарвинской "борьбой за существование":
- скрещиваются (crossover; в русской биологической литературе эта операция традиционно называется кроссинговер),
- порождают разнообразных "детей",
- соперничают за ограниченные ресурсы,
- мутируют
- и, в конечном счете, умирают.
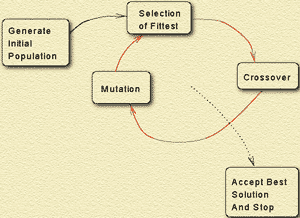
Схема работы генетического алгоритма.
Схема типичного генетического алгоритма представлена на рис. 2. В статье мы обсудим, как работают различные блоки из этой схемы.
Хромосомы
Разработка генетического алгоритма начинается с конструирования двоичной хромосомы, представляющей возможные решения этой задачи. Традиционно генетические алгоритмы используют для этого двоичные строки фиксированной длины. Например, для нашей ЗКВ с четырьмя городами, которые надо поочередно посетить, проще всего было бы выделить по 2 бита на каждый город, получив 8-битовую хромосому. Рисунок 3 поясняет, как записывается информация на такую хромосому. Можно построить множество случайных строк из 8 бит, интерпретируя их как маршруты объезда городов.
Табл. 1. Случайно выбранные хромосомы.
| Chromosome | Meaning |
|---|---|
| 00110010 | Auckland Wellington Auckland Napier |
| 10101100 | Napier Napier Wellington Auckland |
| 10100101 | Napier Napier New Plymouth New Plymouth |
| 01010101 | New Plymouth New Plymouth New Plymouth New Plymouth |
Но эта хромосома слишком проста для ЗКВ любого размера. Один из ее недостатков заключается в том, что большинство двоичных строк из 8 бит не соответствуют допустимым маршрутам. Как видно из таблицы 1, мы можем получить маршруты, проходящие через некоторые города дважды, а через другие - ни разу. Можно было бы рассматривать и такие "не-решения", с тем чтобы настоящие решения вытеснили их в процессе эволюции, но в дальнейшем мы увидим, что это неэффективный путь. Лучше придумать другую кодировку, чтобы любая двоичная строка представляла допустимый (но, конечно, не всегда разумный) маршрут в ЗКВ.
Табл. 2. Случайно выбранные 5-битовые хромосомы.
| Chromosome | Meaning |
|---|---|
| 10111 | Napier Auckland New Plymouth Wellington |
| 00110 | Auckland New Plymouth Napier Wellington |
| 10101 | Auckland New Plymouth Napier Wellingt |
| 01011 | New Plymouth Napier Wellington Auckland |
Вот одна из таких кодировок: первые два бита - номер первого города в маршруте, вторые два бита - номер того из оставшихся трех городов, который посещается вторым, пятый бит определяет выбор из оставшихся двух городов, а на номер последнего, четвертого города битов выделять не нужно. Мы получаем 5-битовую хромосому. В таблице 2 показаны несколько таких хромосом и соответствующих им маршрутов. Заметим, что и здесь возникает небольшая проблема, так как вторые два бита могут представлять четыре различных числа, которые надо сопоставить трем различным городам. С этим можно справиться, решив, что и 11, и 00 соответствуют первому из этих трех городов. Не очень удачное решение, так как оно вдвое повышает шансы наугад выбрать именно этот город, но пока это нам не очень мешает.
Выживание сильнейших
Сконструировав хромосому, мы без всякого труда можем построить 500 случайно выбранных маршрутов в нашей ЗКВ, сгенерировав 500 случайных 5-битовых чисел. Но ведь мы как раз и мечтали свести программирование к минимуму при решении трудных задач. Значит, цель достигнута? Разумеется, это зависит от того, насколько хороши полученные таким путем решения. Другими словами, затратит ли наш коммивояжер минимально возможное время на свои переезды из города в город, если воспользуется некоторыми из предлагаемых маршрутов?
В нашем случае ответ, скорее всего, будет утвердительным. 5 бит могут представлять лишь 32 различных числа, поэтому среди нескольких сот случайных маршрутов, наверное, будет и оптимальный. Пространство поиска возможных решений очень мало. К сожалению, трудные для современных компьютеров ЗКВ относятся к нескольким сотням объектов: например, городов или скважин, которые необходимо пробурить, и т. д. В этом случае объем пространства поиска приближается по порядку величины к числу атомов в известной части вселенной, и, по всей вероятности, даже лучшее из пятисот выбранных наугад решений окажется очень плохим. Вот здесь и начинает работать эволюция.
Нам нужно каким-то образом сымитировать "выживание сильнейших" (survival of the fittest), позволяя лучшим хромосомам жить, а не самых лучших обрекая на гибель. Традиция разработки генетических алгоритмов предписывает выбирать каждое последующее поколение (то есть совокупность определенного количества хромосом) путем стохастической, но целенаправленной селекции. Для этого мы должны знать, как отличить хорошие хромосомы от плохих.
Реализация генетического алгоритма предполагает задание функции приспособленности, или фитнес-функции (fitness function). Эта функция получает на вход двоичную хромосому и возвращает число, показывающее, насколько хороша эта хромосома. В реализованном автором генетическом алгоритме решения ЗКВ сначала определяется наихудшая хромосома (отвечающая самому длинному из маршрутов) и измеряется длина этого маршрута (в километрах). Полученное число умножается на 1,1 и объявляется плохой длиной, по отношению к которой оценивается качество остальных хромосом: приспособленность хромосомы вычисляется как разность между плохой длиной и длиной маршрута, заданного данной хромосомой. В результате этих несколько запутанных вычислений каждой хромосоме ставится в соответствие ее приспособленность (fitness) - число, которое оказывается сравнительно маленьким для плохих (длинных) маршрутов и сравнительно большим для хороших (коротких) маршрутов.
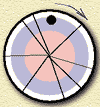
Вернемся к "выживанию сильнейших". Будем использовать "колесо рулетки" для того, чтобы выбрать из текущего поколения хромосомы, которые сохранятся в следующем поколении. Если читатель представляет себе обычную рулетку, он согласится, что у шарика одинаковые шансы остановиться в любом из секторов. Но если рулетка разделена на неравные секторы (рис. 4), вероятность того, что шарик остановится в широком секторе, велика, а в узком - мала. Предположим, что каждый сектор нашей "кривой" рулетки отвечает одной из хромосом, а ширина сектора пропорциональна ее качеству. Запустив рулетку 500 раз, мы получим новое поколение хромосом.
Так как рулетка "кривая", вполне возможно, что некоторые из хромосом данного поколения будут выбраны несколько раз, а некоторые - ни разу. Хотя случайный характер выбора и может привести к отсеву ("смерти") очень хорошо приспособленных хромосом и увеличению количества плохо приспособленных хромосом, в среднем число хороших хромосом будет расти, а плохих - уменьшаться. Можно ожидать, что качество следующей популяции будет, в среднем, выше качества предыдущей. Начинают работать факторы эволюции, так как хромосомы фактически вынуждены бороться за место в следующем поколении под действием "искусственного дефицита" (artificial scarcity).
Кроссинговер (crossover): по-нашему - скрещивание
Однако здесь возникает вопрос: получили ли мы лучшие решения, чем те, что были в предыдущем поколении? Короткий ответ: нет, не получили. Колесо рулетки не создает новых решений. Первое, что нужно для создания таких решений, - кроссинговер (crossover).
При кроссинговере хромосомы группируются в пары, и случайным образом выбирается точка кроссинговера. Например, для наших 5-битовых хромосом мы можем наугад выбрать одну из точек 1, 2, 3, 4. Операция кроссинговера состоит в следующем: мы меняем местами участки выбранных хромосом слева от точки кроссинговера. Это показано на рис. 5 для точки кроссинговера 3.
Кроссинговер смешивает "генетический материал" двух родителей, причем можно ожидать, что приспособленность родителей выше средней в предыдущем поколении, так как они только что прошли очередной раунд борьбы за выживание. Это аналогично соперничеству настоящих живых существ, где лишь сильнейшим удается передать свои (предположительно хорошие) гены следующему поколению. Важно, что кроссинговер может порождать новые хромосомы, ранее не встречавшиеся в популяции.
Не все пары хромосом в новой популяции подвергаются кроссинговеру. Некоторые хромосомы остаются неизменными. Это зависит от того, какой стороной упадет виртуальная монетка, которую подбрасывают для каждой пары. Если выпадает орел (это может происходить с некоторой фиксированной вероятностью - например, 0,1 или 0,3, или 0,6 и т. д.), то происходит кроссинговер со случайно выбранной точкой.
Мутации
Последний этап - мутация (mutation). Даже для больших популяций может оказаться, что не все биты генетического материала в ней представлены. Например, если первый бит у всех хромосом равен 0, то кроссинговер никогда не породит решение с 1 в первом бите. Мутация предназначена для того, чтобы избежать таких ситуаций и увеличить вариабельность популяции. Частота мутации обычно очень низкая - отвечающая за нее виртуальная монетка должна падать орлом вверх один раз за сто или тысячу бросаний. Если выпадает орел, в хромосоме выбирается случайный бит и его значение меняется на противоположное (0 превращается в 1, а 1 - в 0). На рис. 6 показан процесс мутации одной из хромосом.
Процесс поиска решений
Мутация и кроссинговер могут порождать новые решения, которые никогда не встречались в предыдущих поколениях. Для оценки качества этих решений вычисляется фитнес-функция. На этом построение нового поколения решений заканчивается.
При переходе от первого поколения ко второму может появиться решение более высокого качества. Однако и оно, скорее всего, еще не будет приемлемым. Как и в естественной эволюции, одна смена поколений не приводит к заметному прогрессу вида (в нашем случае - набора решений ЗКВ). Поэтому генетический алгоритм создает следующее поколение, последовательно применяя "выживание сильнейшего", кроссинговер и мутацию. Затем таким же образом обрабатывается это новое поколение и так далее. Процесс повторяется тысячи или даже миллионы раз. При этом могут постепенно "выводиться" очень хорошие маршруты путешествия коммивояжера, расписания работы автобусных смен, решения других задач.
Замечательная черта генетических алгоритмов состоит в том, что они выполняют множество изощренных манипуляций с решениями задачи, но без малейшего представления о том, что же при этом происходит! Процедура кроссинговера берет два решения ЗКВ и создает из них два новых решения, смешивая части первого и второго. Все, что для этого нужно, - выбор случайной позиции в битовой строке и перестановка двух подстрок. Та же самая процедура, что манипулирует с решениями ЗКВ, может помочь наилучшим образом рассадить гостей за свадебным столом. Единственное, что нужно знать, - длину двоичной хромосомы. То же самое относится и к процедурам мутации, выживания сильнейшего и даже создания начальной популяции. Благодаря этому свойству достаточно один раз программно реализовать генетический алгоритм (а еще лучше - загрузить уже готовую программу из Интернета), а потом использовать его для решения множества самых разнообразных задач без сколько-нибудь серьезного изменения кода.
Фитнес-функция - это единственная часть программы, которая должна понимать, что же на самом деле кодирует хромосома. Поэтому для каждого приложения надо писать новые фитнес-функции. К счастью, они обычно довольно просты, особенно по сравнению с программой, которая могла бы понадобиться для полного решения задачи. Очень трудно написать программу, дающую хотя бы просто "хорошие" решения больших ЗКВ. Очень легко написать функцию, которая вычисляет длину данного маршрута и вычитает ее из некоего опорного значения. Очень трудно написать программу, которая строит расписания работы экипажей для автобусных компаний. Очень легко написать процедуру, которая подсчитывает количество шоферов и оценивает те расписания, где заняты (читай: оплачиваются) меньше шоферов, выше, чем те, где шоферов нужно больше. Для ряда приложений генетические алгоритмы приближаются к мифической системе, о которой мы упоминали: "дай описание задачи и жди готового решения".
Сравнение ГА с другими методами решения задач
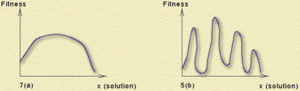
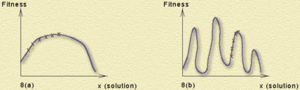
Для того чтобы понять, почему генетические алгоритмы работают, задумаемся над понятием пространства поиска. Пространство поиска - это множество возможных решений задачи. Например, это может быть множество всех возможных расстановок фигур на шахматной доске. Если мы нарисуем график приспособленности решений для простой задачи, мы можем получить как простое и предсказуемое (рис. 7a), так и более сложное (рис. 7b) пространство поиска. И в том, и в другом случае пространство поиска одномерно. Хромосома представляет одно число, которое и описывает решение (например, это может быть температура, при которой лучше всего растут помидоры). Размерность пространства поиска для более сложных задач может достигать нескольких сотен; в этом случае рисовать какие-либо графики невозможно, а программы поиска становятся крайне сложными.
Рассмотрим один из простых методов поиска - метод восхождения (hillclimbing). Он работает так: сначала генерируется случайное решение (например, маршрут в ЗКВ), затем в него вносится "единичное" возмущение (например, меняется местами пара городов), и возмущенное решение сравнивают с исходным. Если новый маршрут короче, он сохраняется, а старый отбрасывается. Если новый маршрут длиннее старого, то сохраняется старый. Затем процесс повторяется с сохраненным решением, но уже с другим единичным возмущением, и так далее. Если в течение, скажем, тысячи итераций решение не улучшается, оно объявляется оптимальным, и процесс останавливается.
При восхождении мы всегда идем вверх (в смысле функционала качества решения). Если пространство поиска простое и содержит лишь один пик приспособленности (рис. 8a), то при помощи восхождения мы найдем оптимальное решение. Если же оно более сложное и мы начинаем восхождение вблизи одного из небольших пиков (локальных максимумов), то глобальный оптимум вряд ли будет найден (рис. 8b). Для его нахождения надо пройти через область плохих решений. Метод восхождения на это не способен.
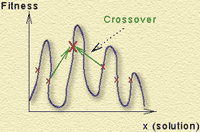
Генетический алгоритм действует более тонко. На рис. 9 мы видим, что генетическая популяция содержит много решений, разбросанных там и сям по пространству поиска. Мутация действует аналогично единичному возмущению в методе восхождения и приводит в основном к блужданию вблизи того пика, на котором находится решение. Однако операция кроссинговера порождает новые точки, которые могут попадать на удаленные пики, как показано на рис. 9. В этом отличие генетических алгоритмов от более простых, таких как восхождение. Генетический алгоритм эффективно просматривает пространство поиска, сохраняя хороших родителей, которые чаще, чем плохие, дают хорошее потомство. Поэтому такой алгоритм с большей вероятностью найдет хорошее решение задачи - например, симпатичный короткий маршрут в ЗКВ.
Теперь можно объяснить, почему мы не стали использовать первое, что пришло в голову, а именно 8-битовые хромосомы, допускавшие запрещенные решения, а сконструировали более сложные, 5-битовые. Было бы нетрудно построить фитнес-функцию, которая бы заведомо оценивала все допустимые решения выше, чем запрещенные. Генетический алгоритм мог бы тогда искать "наилучшие" решения, которые предположительно оказались бы допустимыми (то есть давали бы маршруты, проходящие через все города ровно по одному разу). Но плохо то, что размерность пространства поиска сильно возросла бы. Вместо 32 возможных решений для нашей ЗКВ с четырьмя городами нам пришлось бы рассматривать в 8 раз больше, то есть 256 возможных решений. А объем пространства поиска - важнейший, хотя и не единственный фактор, влияющий на качество работы генетического алгоритма. Большие пространства труднее "обыскать", и шансы найти оптимальное или просто хорошее решение уменьшаются. Конструкция хромосомы, уменьшающая объем пространства поиска, повышает эффективность генетического алгоритма. Для больших ЗКВ с сотнями городов наша наивная конструкция хромосомы неприемлема - алгоритм занимался бы только поиском допустимого решения, а до поиска хорошего решения дело бы вообще не дошло! Конструирование хромосомы обычно является самым важным этапом создания генетического алгоритма.
Улучшение алгоритма - нестандартный кроссинговер
Для работы с 5-битовой хромосомой необходимо чуть больше программирования, чем для работы с 8-битовой. За счет усложнения программы алгоритм можно улучшить и другим способом - применяя нестандартный кроссинговер. Метод "жадной генетики" (greedy genetics) вместо кроссинговера в случайной точке использует "жадный алгоритм" (greedy algorithm) для получения "хорошего" потомства.
Жадные алгоритмы применяются в самых разных задачах. Они являются, в сущности, реализацией в той или иной конкретной обстановке следующих абстрактных советов:
- - оцените все возможности улучшить данное решение;
- - выберите ту, при которой улучшение максимально;
- - используйте ее;
- - действуйте так до тех пор, пока не будет найдено приемлемое решение.
Жадное решение в применении к ЗКВ может выглядеть так.
- 1) Выберите произвольный город; он становится одновременно и начальным, и конечным пунктом маршрута.
- 2) Пока список городов не исчерпан, делайте следующее:
- - Найдите город, ближайший либо к начальному, либо к конечному пункту.
- - Добавьте новый город к новому маршруту: в конец, если он ближайший к конечному пункту, или в начало, если он ближайший к начальному пункту.
- - Найдите город, ближайший либо к начальному, либо к конечному пункту.
- 3) Запишите полученное решение.
Надежда получить очень хороший маршрут основана здесь на том, что на каждом шаге мы выбираем города, близкие друг к другу. Однако задачи типа ЗКВ часто оказываются слишком сложными для этого метода, а решения, найденные этим жадным алгоритмом, слишком плохими.
В жадной генетике на кроссинговер накладывается дополнительное условие: все сегменты (то есть отрезки маршрута, соединяющие два города) маршрутов-детей должны встречаться у одного из родителей. В результате качество детей обычно не уступает качеству родителей или превосходит его, и эволюция существенно ускоряется. Даррел Уайтли (Darrell Whitely) применил жадную генетику к ЗКВ и получил хорошие результаты [1]. Автор данной статьи использовал жадную генетику в задаче составления графиков работы сменных экипажей автобусов и тоже получил хорошие результаты [2]. Один из недостатков жадной генетики в том, что за счет ускорения эволюции алгоритм быстро находит приемлемое решение там, где обычный генетический алгоритм нашел бы лучшее решение, хотя и за более длительное время. В своих исследованиях я стремился вернуть как можно больше стохастики в процедуру кроссинговера, сохранив тот "рывок вперед", который дает жадная стратегия. Эксперименты убедили меня, что случайная составляющая совершенно необходима генетическим алгоритмам; без нее они работают гораздо хуже.
Когда использовать ГА?
И в заключение остановимся на том, когда же следует использовать генетические алгоритмы. В одних обстоятельствах они хороши, в других - не очень. В общем случае генетические алгоритмы не находят оптимального решения очень трудных задач. Если оптимальное решение задачи (например, ЗКВ с очень большим числом городов) не может быть найдено традиционными способами - например, методом сцепления ветвей (branch and bound method), - то и генетический алгоритм вряд ли найдет оптимум. С другой стороны, вполне возможно, что генетический алгоритм найдет достаточно хорошее решение. В конце концов, коммивояжеру в любом случае надо ехать продавать свои товары, даже если мы не уверены в абсолютной оптимальности маршрута! Но есть примеры, когда в очень трудных задачах, в том числе и в ЗКВ, с помощью генетических алгоритмов были получены очень хорошие решения.
В двух случаях генетические алгоритмы очень хороши. Первый случай: когда не известен способ точного решения задачи. Если мы знаем, как оценить приспособленность хромосом, то всегда можем заставить генетический алгоритм решать эту задачу. Второй случай: когда способ для точного решения существует, но он очень сложен в реализации, требует больших затрат времени и денег, то есть, попросту говоря, дело того не стоит. Пример - создание программы для составления персонального расписания на основе техники покрытия множеств с использованием линейного программирования.
Несмотря на то, что конструирование хромосом и фитнес-функций может потребовать значительных усилий, генетические алгоритмы легко реализуются даже с нуля и способны решать широкий круг задач. Используя аналогию с развитием живых организмов от простых форм к более сложным, генетические алгоритмы приблизились к тому, чтобы стать общим методом решения задач. Другие "природоподобные" парадигмы, такие как моделирование отжига (simulated annealing) и табу-поиск (taboo search), тоже позволяют решать аналогичные задачи. Но что может сравниться с чувством, которое вы испытываете, глядя на результат работы генетического алгоритма и невольно спрашивая себя: "Неужели все это могло образоваться лишь по воле случая?"
Ссылки
- Genetic Operators, the Fitness Landscape and the Traveling Salesman Problem, D.Whitley and K. Mathias, Parallel Problem Solving from Nature-PPSN 2. R. Mainner and B Manderick, eds., pp. 219-228. North Holland-Elsevier, 1992.
- R.P.Clement & A.Wren, "Genetic Algorithms and Bus-Driver Scheduling".Presented at the 6th International Conference for Computer-Aided Transport Scheduling, Lisbon, Portugal, 1993.
http://www.ing.unlp.edu.ar/cetad/mos/TSPBIB_home.html - страница, посвященная ЗКВ (TSPBIB homepage).
http://www.aic.nrl.navy.mil/galist - архив генетических алгоритмов.
http://aif.wu-wien.ac.at/~geyers/archive/gpk/vuegpk.html - реализация генетического алгоритма на C++.
http://www4.ncsu.edu/eos/users/d/dhloughl/public/stable.htm - Java-апплет генетического алгоритма.
http://www.lalena.com/ai/tsp - генетический алгоритм для ЗКВ.
http://megaswf.com/serve/102223/ - визуальный пример пример работы генетического алгоритма
http://www.computerra.ru/offline/1999/289/2523/ - Эта статья была опубликована в журнале "Компьютерра" , 1999.