Определение координат робота по локальным координатам маяков — различия между версиями
=DeaD= (обсуждение | вклад) |
Delphi (обсуждение | вклад) (Добавлен пример использования) |
||
| (не показано 10 промежуточных версий 2 участников) | |||
| Строка 3: | Строка 3: | ||
== Недостатки метода триангуляции и аналогичных "точных" методов == | == Недостатки метода триангуляции и аналогичных "точных" методов == | ||
| + | [[Изображение:RobotPos Triangle.png|thumb|300px|Схема метода триангуляции|right]] | ||
| + | Классические подходы к определению глобальных координат обычно опираются на метод триангуляции или что-то в этом роде. | ||
| − | + | Метод триангуляции позволяет определить положение робота, решив треугольник (строго говоря, не один). А именно, зная расстояние между маяками-реперами (на рисунке обозначено как ''base''), а так же имея измеренные расстояния до реперов (''dist_1'' и ''dist_2''), мы можем определить положение робота. Как решать треугольники см. [http://www.college.ru/mathematics/courses/planimetry/design/index.htm соответствующую статью] в разделе "Планиметрия" обучающего сайта. | |
| + | Одного треугольника не достаточно для точного определения положения робота, т.к. зная измеренные расстояния ''dist_1'' и ''dist_2'' и базу маяков ''base'' мы получаем две точки равновероятного положения робота. Вторую точку на рисунке можно найти, отразив треугольник относительно линии '''base'''. | ||
| + | |||
| + | На практике часто вместо достаточной для триангуляции и точной информации, мы имеем избыточную, но неточную, а поэтому противоречивую информацию. Например, мы знаем что расстояние между маяками 1 и 2 составляет 10м, но наши сенсоры выдали нам ответ, что расстояние до маяка 1 составляет 4 метра, а до маяка 2 расстояние 5 метров. В этом случае очевидно что мы имеем погрешность измерения расстояния до маяков минимум 0.5м. Если мы можем с хорошей точностью оценивать погрешность каждого известного нам параметра, то это в значительной степени может нам из массы неточной информации получить более-менее точные глобальные координаты, как это делается - читайте ниже. | ||
== Поиск глобальных координат робота через минимизацию функции "неправдоподобия" == | == Поиск глобальных координат робота через минимизацию функции "неправдоподобия" == | ||
| Строка 21: | Строка 26: | ||
** Расстояние от робота до известных объектов; (измеренное расстояние - Di, погрешность - DPi единиц длины) | ** Расстояние от робота до известных объектов; (измеренное расстояние - Di, погрешность - DPi единиц длины) | ||
** Локальные координаты маяков относительно робота; (измеренные координаты - Xi,Yi, погрешность - ZPi единиц длины) | ** Локальные координаты маяков относительно робота; (измеренные координаты - Xi,Yi, погрешность - ZPi единиц длины) | ||
| − | ** Глобальные координаты робота (GPS / другие готовые системы); (измеренные координаты - GXi,GYi, погрешность GZPi единиц длины) | + | ** Глобальные координаты робота (GPS / энкодеры / другие готовые системы); (измеренные координаты - GXi,GYi, погрешность GZPi единиц длины) |
| Строка 32: | Строка 37: | ||
То есть мы просто ищем наиболее правдоподобные координаты и направление робота, учитывая имеющуюся у нас информацию и сведения о точности этой информации. | То есть мы просто ищем наиболее правдоподобные координаты и направление робота, учитывая имеющуюся у нас информацию и сведения о точности этой информации. | ||
| − | + | === Типовые компоненты Xi,Yi === | |
| − | === Типовые компоненты | + | Если мы замерили локальные координаты (XLOCi,YLOCi) относительно робота объекта, чьи глобальные координаты известны как (XOi,YOi), тогда i-я компонента функции "неправдоподобия" координат робота (X,Y,A) соответствующая этой информации будет считаться как Di=(X+XLOCi*cos(A)-YLOCi*sin(A)-XOi)^2+(Y+YLOCi*cos(A)+XLOCi*sin(A)-YOi)^2. (вроде не ошибся(?)) |
| − | |||
| − | |||
=== Поиск минимума полученной функции === | === Поиск минимума полученной функции === | ||
| − | + | Мы будем пользоваться доступной нам вычислительной мощность и часть задачи решим перебором, а именно - мы будем перебирать все возможные углы ориентации робота, а искать аналитическим методом будем только координаты. А при выбранной гипотезе по текущему направлению робота функция неправдоподобия примет вид F(x,y)=A*x^2+B*x+C*y^2+D*y+E, соответственно минимум её находится в координатах x0,y0, являющихся решениями уравнений F'x=0, F'y=0, то есть 2*A*x+B=0, 2*C*y+D=0. | |
=== Пример использования метода === | === Пример использования метода === | ||
| − | + | Маяковая система навигации, определяющая положение роботов по 3м маякам с известными координатами. Полностью автономная, с промышленным протоколом.Описание системы вы можете найти здесь http://robot-develop.org/archives/484 | |
| + | Эта система применялась для навигации мобильного автономного робота проекта Евробот 2011. | ||
Текущая версия на 23:26, 26 февраля 2011
Содержание
[убрать]Недостатки метода триангуляции и аналогичных "точных" методов
Классические подходы к определению глобальных координат обычно опираются на метод триангуляции или что-то в этом роде.
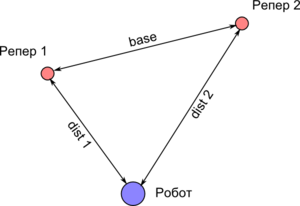
Метод триангуляции позволяет определить положение робота, решив треугольник (строго говоря, не один). А именно, зная расстояние между маяками-реперами (на рисунке обозначено как base), а так же имея измеренные расстояния до реперов (dist_1 и dist_2), мы можем определить положение робота. Как решать треугольники см. соответствующую статью в разделе "Планиметрия" обучающего сайта.
Одного треугольника не достаточно для точного определения положения робота, т.к. зная измеренные расстояния dist_1 и dist_2 и базу маяков base мы получаем две точки равновероятного положения робота. Вторую точку на рисунке можно найти, отразив треугольник относительно линии base.
На практике часто вместо достаточной для триангуляции и точной информации, мы имеем избыточную, но неточную, а поэтому противоречивую информацию. Например, мы знаем что расстояние между маяками 1 и 2 составляет 10м, но наши сенсоры выдали нам ответ, что расстояние до маяка 1 составляет 4 метра, а до маяка 2 расстояние 5 метров. В этом случае очевидно что мы имеем погрешность измерения расстояния до маяков минимум 0.5м. Если мы можем с хорошей точностью оценивать погрешность каждого известного нам параметра, то это в значительной степени может нам из массы неточной информации получить более-менее точные глобальные координаты, как это делается - читайте ниже.
Поиск глобальных координат робота через минимизацию функции "неправдоподобия"
Мы будем рассматривать ситуацию в которой у нас избыточная или достаточная информация, из которой мы можем с некоторой точностью назвать наши координаты и, возможно, направление.
Попробуем теперь понять, информация какого сорта может у нас оказаться:
- С погрешностью измеряемой в единицах угла:
- Ориентация робота глобальная (компас, звезды); (измеренный угол - GAi, погрешность GAPi единиц угла);
- Ориентация робота локальная (известные объекты на карте); (измеренный угол - Ai, погрешность APi единиц угла);
- С погрешностью измеряемой в единицах длины:
- Расстояние от робота до известных объектов; (измеренное расстояние - Di, погрешность - DPi единиц длины)
- Локальные координаты маяков относительно робота; (измеренные координаты - Xi,Yi, погрешность - ZPi единиц длины)
- Глобальные координаты робота (GPS / энкодеры / другие готовые системы); (измеренные координаты - GXi,GYi, погрешность GZPi единиц длины)
В первую очередь мы должны определиться с тем, как будем соотносить погрешности угла и длины, то есть погрешность в сколько единиц длины для нас так же важна как погрешность в одну единицу угла. Далее будем называть эту величину K0. Кроме того - условимся, что все погрешности ненулевые (нет абсолютно точных приборов дающих информацию с бесконечной точностью, даже если прибор не дает неправильного ответа, у него все равно есть шаг деления, и точность - минимум половина этого шага).
Далее мы введем функцию "неправдопободия глобальных координат и направления робота" F(x,y,a) и вся работа будет сведена к минимизации этой функции. Наиболее простой и общепринятый подход к определиню такой функции - принять за неё сумму взвешенных квадратов отклонений (Wi*Di)^2 ожидаемого значения параметров при расположении робота (x,y,a) от наблюдаемого. Вес Wi каждого отклонения - 1/(погрешность соответствующего измерения параметра) для отклонений в единицах длины и K0/(погрешность соответствующего измерения параметра) для отклонений в единицах угла. При этом каждое Di есть функция 3 параметров - x,y,a - координат и направления робота.
То есть мы просто ищем наиболее правдоподобные координаты и направление робота, учитывая имеющуюся у нас информацию и сведения о точности этой информации.
Типовые компоненты Xi,Yi
Если мы замерили локальные координаты (XLOCi,YLOCi) относительно робота объекта, чьи глобальные координаты известны как (XOi,YOi), тогда i-я компонента функции "неправдоподобия" координат робота (X,Y,A) соответствующая этой информации будет считаться как Di=(X+XLOCi*cos(A)-YLOCi*sin(A)-XOi)^2+(Y+YLOCi*cos(A)+XLOCi*sin(A)-YOi)^2. (вроде не ошибся(?))
Поиск минимума полученной функции
Мы будем пользоваться доступной нам вычислительной мощность и часть задачи решим перебором, а именно - мы будем перебирать все возможные углы ориентации робота, а искать аналитическим методом будем только координаты. А при выбранной гипотезе по текущему направлению робота функция неправдоподобия примет вид F(x,y)=A*x^2+B*x+C*y^2+D*y+E, соответственно минимум её находится в координатах x0,y0, являющихся решениями уравнений F'x=0, F'y=0, то есть 2*A*x+B=0, 2*C*y+D=0.
Пример использования метода
Маяковая система навигации, определяющая положение роботов по 3м маякам с известными координатами. Полностью автономная, с промышленным протоколом.Описание системы вы можете найти здесь http://robot-develop.org/archives/484 Эта система применялась для навигации мобильного автономного робота проекта Евробот 2011.