Перевод статьи "Просто о ПИД-алгоритмах" — различия между версиями
=DeaD= (обсуждение | вклад) (→Дифференциальное управление) |
=DeaD= (обсуждение | вклад) (→Дифференциальное управление) |
||
| Строка 351: | Строка 351: | ||
Когда вы используете дифференциальное управление нужно обращать внимание на точность временных интервалов между итерациями управляющего цикла. Я рекомендую поддерживать точность этих интервалов в пределах 1%, однако чем точнее, тем лучше. Если вы не можете обеспечить это на аппаратном уровне - постарайтесь сделать это на уровне программного обеспечения, отдав под задачу сбора информации максимальный приоритет (не нужно с такой точностью выполнять расчеты управляющего воздействия, достаточно собирать информацию в нужные моменты времени). Один из оптимальных вариантов - поместить сбор информации о системе в прерывание, а сами расчеты ПИД-алгоритма выполнять в свободное время. | Когда вы используете дифференциальное управление нужно обращать внимание на точность временных интервалов между итерациями управляющего цикла. Я рекомендую поддерживать точность этих интервалов в пределах 1%, однако чем точнее, тем лучше. Если вы не можете обеспечить это на аппаратном уровне - постарайтесь сделать это на уровне программного обеспечения, отдав под задачу сбора информации максимальный приоритет (не нужно с такой точностью выполнять расчеты управляющего воздействия, достаточно собирать информацию в нужные моменты времени). Один из оптимальных вариантов - поместить сбор информации о системе в прерывание, а сами расчеты ПИД-алгоритма выполнять в свободное время. | ||
| − | + | Дифференциальное управление страдает от шумов больше других типов управления потому что оно эти шумы усиливает, в отличие от пропорционального управления, которое просто транслирует эти шумы или интегрального, которое вообще шумы подавляет. Посмотрите на коэффициенты дифференциальной компоненыт, которые я использовал выше и представьте, что произойдёт если у вас в системе будут небольшие шумы, которые возникать при каждом получении информации о системе. Умножьте эти небольшие шумы на коэффициент 2000 и представьте как это отразится на системе. | |
| − | + | Вы можете применить фильтрацию дифференциальной компоненты управления, но это существенно снизит её полезность. Теория стоящая за тем, как это делать и как опредилить - будет ли это работать останется за рамками этой вводной статьи. Возможно лучшее, что вы можете сделать с этой проблемой - is to look at how likely you are to see any noise, how much it will cost to get quiet inputs, and how badly you need the high performance that you get from differential control. Once you've worked this out, you can avoid differential control altogether, talk your hardware folks into getting you a lower noise input, or look for a control systems expert. | |
The full text of the PID controller code is shown in Listing 1 and is available at www.embedded.com/code.html. | The full text of the PID controller code is shown in Listing 1 and is available at www.embedded.com/code.html. | ||
Версия 16:07, 3 августа 2008
Автор: Tim Wescott
Перевод начал: Ботов Антон aka =DeaD=
Содержание
- 1 Введение
- 2 ПИД управление
- 3 Объекты управления
- 4 Двигатель с редуктором
- 5 Безконтактная система сверхточного позиционирования
- 6 Термосистема
- 7 Контроллеры
- 8 Пропорциональное управление
- 9 Интегральное управление
- 10 Дифференциальное управление
- 11 Tuning
- 12 Other issues
- 13 Sampling rate
- 14 Exert control
Введение
Алгоритмы ПИД (PID = proportional, integral, derivative) управления не так сложны, как кажется некоторым с первого взгляда. В этой статье мы попробуем рассказать как они работают на нескольких простых примерах. Изучив эти примеры, вы сможете самостоятельно применять эти алгоритмы в своих проектах.
Моя профессиональная деятельность непосредственно связана с реализацией управляющих циклов в программном обеспечении для различных устройств. Исходя из накопленного опыта, могу сказать, что не смотря на огромное количество алгоритмов и методов управления, которыми я владею - большая часть проблем такого сорта решается простейшими контроллерами без привлечения полного аппарата теории управления. В этой статье я расскажу, как реализовать и настроить простейший контроллер использующий ПИД-алгоритм без привлечения сложного математического аппарата и длительного изучения теории управления. Приведенная в статье техника настройки контроллера является проверенным и зарекомендовавшим себя методом, который можно успешно применять на большинстве задач управления.
ПИД управление
PID=ПИД означает "proportional=пропорциональный", "integral=интегральный", "derivative=дифференциальный". Эти три термина описывают простейшие элементы ПИД-контроллера. Каждый из этих элементов выполняет свою задачу и оказывает свое специфическое воздействие на функционирование системы.
В типичном ПИД-контроллере эти элементы оперируют комбинацией как входных управляющих параметров, так и сигналами обратной связи с управляемого устройства (объекта управления, далее просто - устройство). Выходы этих элементов складываются между собой и формируют управляющий сигнал для устройства.
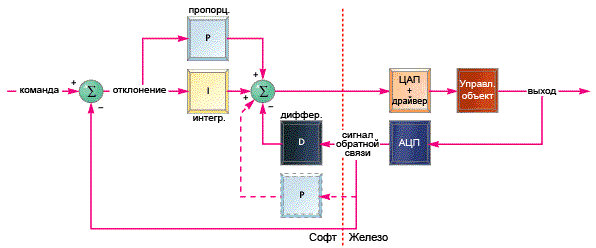
Рисунок 1. Простейший ПИД-контроллер
В приведенном на рисунке примере дифференциальный элемент оперирует только
сигналом обратной связи от устройства. Этот сигнал вычитается из сигнала
управляющего воздействия и полученная разность считается ошибкой управления.
Эта разность подается на вход пропорциональному и интегральным элементам,
получающиеся на их выходах сигналы складываются между собой и формируют
управляющий сигнал. Я не описывал принцип работы этих элементов - мы вернемся
к этому чуть позже. На схеме я указал альтернативный вариант включения
пропорционального элемента (пунктиром) - оптимальную схему включения можно
выбрать только на конкретном устройстве и задаче управления.
Объекты управления
Чтобы в обсуждении темы не уходить далеко от реальных задач нам понадобятся типичные объекты управления. В этой статье я буду использовать для примеров следующие три устройства, и покажу как на них будут работать те или иные алгоритмы ПИД-управления:
- Двигатель с редуктором;
- Безконтактная система сверхточного позиционирования;
- Термосистема;
Каждая из этих систем имеет различные характеристики и требует различных подходов в управлении для достижения оптимальных результатов.
Двигатель с редуктором
Первым рассмотрим двигатель с редуктором, на выходном валу которого установлен потенциометр или любым другим датчиком положения вала. Такое решение применяется в устройствах позиционирования печатной головки в струйных принтерах, или в системе управления дроссельной заглушкой в автомобильной системе круиз-контроля (поддержание заданной скорости на трассе), или в любой другой современной системе управления точным позиционированием.
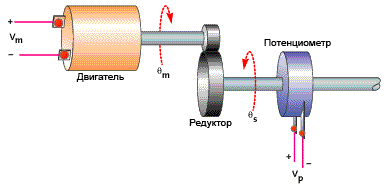
Рисунок 2. Схема управления двигателем с редуктором
Двигатель управляется уровнем напряжения задаваемым управляющим алгоритмом.
Усилие через редуктор поступает на его выходной вал и приводит в действие
некоторый механизм. На выходном валу находится потенциометр, через который
алгоритм управления получает информацию о положении выходного вала.
Коллекторный двигатель постоянного тока вращается с постоянной скоростью пропорциональной поданному напряжению. Реальный двигатель с редуктором не могут мгновенное изменять скорость вращения, поэтому между подачей на двигатель напряжения и установлением соответствующей скорости существует некоторая задержка. Редуктор в этой схеме просто умножает скорость вращения двигателя на некоторую константу.
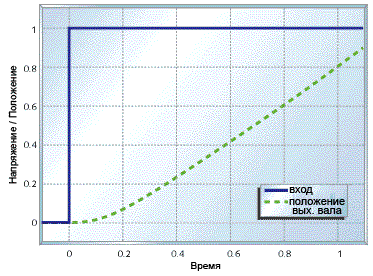
Рисунок 3. График положения вала при старте
На рисунке показано поведение системы при подаче некоторого фиксированого
напряжения в момент времени t = 0 (мы рассматриваем общие примеры, поэтому
примем напряжение в 1). Из графика видно, что мотор не сразу набирает
соответствующую напряжению скорость, но после того, как набрал (при t=0.2),
дальше он её поддерживает.
Безконтактная система сверхточного позиционирования
В некоторых случаях необходимо с сверхвысокой точностью управлять положением некоторого объекта. Систему, решающую эту задачу, можно построить из свободно перемещающейся механической платформы, пары "катушка + магнит" (аналогичной применяющимся в громкоговорителях) и безконтактного датчика положения. Такие решения применяются в механизмах оптической стабилизации в фото/видеотехнике, или в других системах, где нужно с высокой точностью перемещать небольшой элемент устройства.
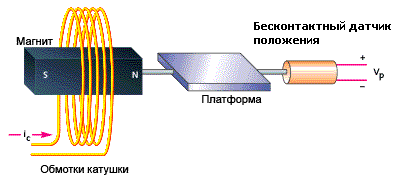
Рисунок 4. Безконтактная система сверхточного позиционирования
Программное обеспечение управляет подачей тока на обмотки катушки, который
создает магнитное поле соответствующей плотности и направления, которое
втягивает или выталкивает магнит вместе с платформой, на которой он закреплен.
Обратную связь по положению платформы обеспечивает безконтактный датчик.
При таком устройстве сила, прикладываемая к магниту не зависит от положения платформы и её движения. Плюс этого в том, что платформа ни от каких других воздействий не движется относительно всего устройства, а минус в том, что платформа становится очень неустойчивой, что затрудняет задачу управления. В добавок к этом нам окажется необходим усилитель с большим выходным током и высокоточный безконтактный датчик, что тоже может создать дополнительные трудности в проекте. Создание качественной и надежной системы такого типа достаточно проблемно без применения высокоточного оборудования и тщательного проектирования.
Уравнения, описывающие движение такой системы достоточно просты. Сила, действующая на платформу пропорциональна только уровню напряженности магнитного поля, а значит силе тока, протекающего через катушку. Таким образом ускорение платформы прямо пропорционально управляющему воздействию. График движения платформы при подаче фиксированного ненулевого управляющего воздействия это парабола:
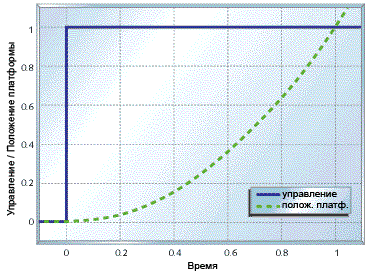
Рисунок 5. График движения при фиксированном воздействии
Как мы увидим позже - такое поведение платформы создаст дополнительные проблемы,
ввиду инертности, из-за которой она не сразу начинает двигаться, а также
стремится продолжить начатое движение.
Термосистема
В этом примере вместо двигателя мы будем использовать нагреватель.
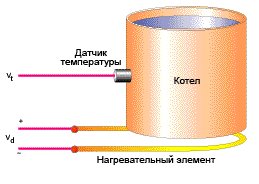
Рисунок 6. Типичная термосистема
Котел снабжен электрическим нагревателем, температура содержимого котла отслеживается с помощью соответствующего датчика температуры.
Вообще математические модели термосистем достаточно сложны, однако в нашем примере мы примем значительно упрощенную модель поведения такой системы. В той части случаев, когда вам не нужно получить выдающихся результатов обычно можно пользоваться менее точными моделями.
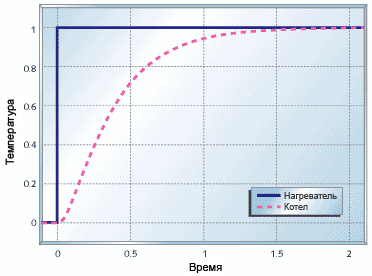
Рисунок 7. График поведения термосистемы при нагреве котла
Рисунок 7 показывает зависимость поведения системы от изменения Vd. Я использовать константы времени t1 = 0.1с и t2 = 0.3с. Как видно в итоге система приходит к требуемому состоянию, но это занимает очень много времени. Кроме того, без значительной теплоизоляции термосистемы очень чуствительны к внешнему воздействию. Этот эффект не показан в приведенном примере, но мы в этой статье позже рассмотрим его подробней.
Контроллеры
Элементы представляемого здесь ПИД-контроллера получают вход либо с датчика состояния управляемой системы, либо с датчика отклонения состояния системы от требуемого. Я буду писать код управляющего контроллера используя арифметику с плавающей точкой, чтобы не отвлекаться в этой статье на вопросы технической реализации, если вам нужно - вы можете легко адаптировать все приведенные здесь примеры к арифметике с фиксированной точкой.
Я буду предполагать, что всё функция управления будет определена нижеуказанным способом. По мере продвижения по тексту статьи вы увидите, как будет вырисовываться содержимое передаваемой структуры данных и внутренности функции.
<source lang="c"> double UpdatePID(SPid * pid,
double error, double position)
{
. . .
} </source>
Причина по которой я передаю в процедуру управления отклонение от целевого состояния, а не состояние системы заключается в том, что иногда нам будет полезно как-то "поиграть" с этим параметром. Поэтому оставление рассчета отклонения в основном коде, вне нашей функции, делает нашу функцию более универсальной. В коде эта функция может быть использована, например, так:
<source lang="c">
. . position = ReadPlantADC(); drive = UpdatePID(&plantPID, plantCommand - position, position); DrivePlantDAC(drive); . .
</source>
Пропорциональное управление
Пропорциональное управление является самым легким в реализации и наиболее часто используется в управляющих циклах. Пропорциональный контроллер просто берет отклонение, умножает его на константу и выдает его в качестве управляющего воздействия. Пропорциональный компонент в контроллере рассчитывается кодом следующего вида:
<source lang="c">
double pTerm; . . . pTerm = pid->pGain * error; . . . return pTerm;
</source>
Рисунок 8 показывает что происходит, когда пропорциональное управление применяется к системе двигателя с редуктором.
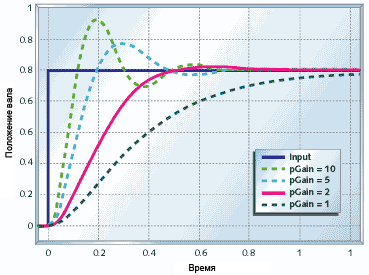
Рисунок 8. Пропорциональное управление двигателем с редуктором
Для малого значения коэффициента (pGain = 1) двигатель приходит к нужному положению, но достаточно медленно. Увеличение коэффициента (pGain = 2) приводит к более быстрой реакции системы. Однако если дальше увеличивать коэффициент (pGain = 5, pGain = 10), то двигатель конечно более быстро достигает требуемого положения, но дальше идёт "перелёт", из-за чего система не приходит к требуемому положению быстрее, чем при меньших коэффициентах. Если мы продолжим увеличивать коэффициент, то мы достигнем ситуации, когда система станет бесконечно осциллировать (колебаться) вокруг заданной точки и никогда не придет в нужное состояние.
Система двигателя с редуктором "перелетает" необходимое положение при больших коэффициентах из-за задержки с реакцией на управляющее воздействие. Если вы вернетесь к рисунку 2, то вы увидите, что двигатель не сразу начинает вращаться при подаче на него управляющего сигнала. Эта задержка, плюс задержка обратной связи по датчику - вот что приводит к "перелёту" через требуемое положение на рисунке 8.
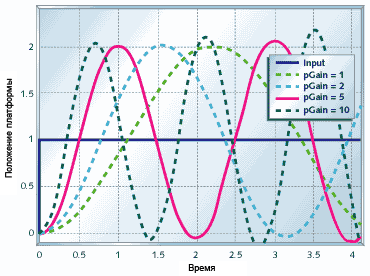
Рисунок 9. Пропорциональное управление системой сверхточного позиционирования
Рисунок 9 показывает как действует пропорциональное управление на систему сверхточного поцизионирования. Как видно этот метод управления в чистом виде вообще не помогает в случае этой задачи. Система обладает настолько большой задержкой восприятия управляющего воздействия, что неважно насколько малый коэффициент вы выберите - система всё равно будет осциллировать. С ростом коэффициента просто увеличивается частота колебаний, но система не приходит в требуемое состояние.
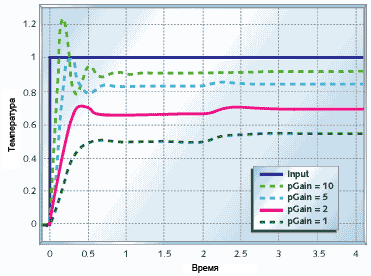
Рисунок 10. Пропорциональное управление термосистемой
Рисунок 10 показывает что происходит, когда вы строите контроллеру температуры на основе метода пропорционального управления. Кроме всего прочего на графиках я показал реакцию системы на внешнее воздействие в виде повышения температуры окружающей среды в момент времени t=2с. Однако видно, что независимо от этого воздействия пропорциональное управление не позволяет установить желаемую температуру. Увеличение коэффициента помогает, но даже при pGain=10 температура котла остается ниже требуемой, и вы начинаете наблюдать сильные "перелёты" через требуемую величину, которые продолжаются без конца (это называется "ringing").
Как видно из приведенных выше примеров пропорцинальное управление даже в одиночку может быть полезно для ряда задач, однако так происходит не всегда. Системы в которых существует значительная задержка реакции на управляющее воздействие, такие как система сверхточного позиционирования, не могут быть стабилизированы с помощью этого метода. Некоторые системы, типа рассмотренного контроллера температуры вообще не достигают требуемого положения. Системы типа двигателя с редуктором вполне работоспособы под таким управлением, но может потребоваться меньшее время вывода системы на требуемое состояние. Чтобы решить все эти проблемы нам потребуется добавить интегральную или дифференциальную составляющу, или обе одновременно.
Интегральное управление
Интегральное управление используется, чтобы добавить "долгосрочной точности" управляющему циклу. Оно практически всегда используется совместно с пропорциональным управлением.
Реализующий интегратор код приведен ниже. Состояние интегратора iState является суммой всех предыдущих входов. Параметры iMin и iMax это минимально и максимально разрешенные значения состояния интегратора.
<source lang="c"> double iTerm;
. . .
// calculate the integral state // with appropriate limiting
pid->iState += error; if (pid->iState > pid->iMax) pid->iState = pid->iMax; else if (pid->iState
<
pid-> iMin) pid->iState = pid->iMin; iTerm = pid->iGain * iState; // calculate the integral term . . .
</source>
Интегральное управление само по себе обычно снижает стабильность системы или вообще делает систему нестабильной.
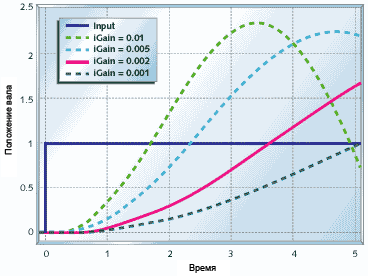
Рисунок 11. Интегральное управление двигателем с редуктором
На рисунке 11 приведены результаты управления двигателя с редуктором контроллером реализующим чисто интегральное управление (pGain = 0). Как видно система вообще не стабилизируется. Как и в случае с системой сверхточного позиционирования с пропорциональным управлением у двигателя с редуктором под чистым интегральным управлением колебания будут становиться только больше и больше, пока это во чтонибудь не упрётся (хорошо если это будет программное ограничение, а не разрушение механической системы).
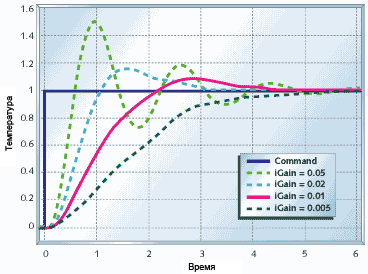
Рисунок 12. Интегральное управление термосистемой
Рисунок 12 показывает как себя ведёт термосистема под чистым интегральным управлением. Как видно время стабилизации системы стано значительно больше, чем при пропорциональном управлении (см. рисунок 10), но зато теперь система стабилизируется при требуемом состоянии, даже при некоторых внешних воздействиях. Если вам не требуется малое время выхода на требуемое состояние - этот метод вам вполне подойдет.
Из последнего графика ясно, как используется интегральный компонент управления. В состоянии интегратора "запоминается" всё что произошло в предыдущие моменты времени и это позволяет контроллеру избегать "долгосрочных ошибок", т.е. поведения при котором мы видим что не достигли требуемого положения, а никакого управляющего воздействия не вносим. Однако у этой медали есть и обратная сторона - контроллер всегда реагирует с некоторым запозданием, когда система уже длительное время получает совершенно неправильные команды. Чтобы стабилизировать предыдущие две системы нам потребуется добавить в принятие решения немного информации о текущем состоянии системы, которое мы имеем в пропорциональной компоненте
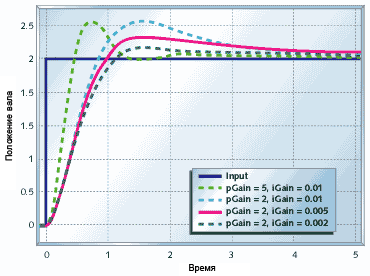
Рисунок 13. Пропорционально-интегральное управление двигателем с редуктором
Рисунок 13 показывает как ведёт себя двигатель с редуктором под пропорционально-интегральном (ПИ) управлением. Сравните это с рисунками 8 и 11. Время на стабилизацию увеличилось по сравнению с чисто пропорциональной схемой, но стабилизация идёт в правильное положение, которе и требовалось.
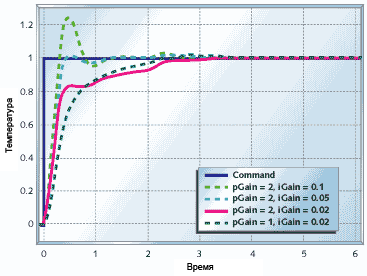
Рисунок 14. Пропорционально-интегральное управление термосистемой
Рисунок 14 показывает, что будет происходить, если применить к термосистеме ПИ-управление. Котёл так же придёт к требуемой температуре, как и в случае чистого интегрального управления (см. рисунок 12), но с ПИ-управлением произойдёт это в два-три раза быстрее. График показывает время стабилизации до требуемой температуры близкое к возможному пределу достигаемому с помощью ПИ-регуляторов на такого типа системах.
Перед тем, как мы закончим рассматривать интеграторы, я хотел бы указать на следующие два важных момента. Во-первых, так как вы добавили интеграцию отклонения по времени, становится важным частота с которой вы запускаете цикл управления. Во-вторых нужно быть внимательным к допустимому диапазону значений интегратора, чтобы избежать "вылетания".
Скорость изменения состояния интегратора равна среднему отклонению умноженному на коэффициент интегратора умноженному на частоту цикла управления. Так как интегратор сглаживает замеры отклонения по времени, допустимы некотороые отклонения от нормальной частоты вызова управляющего цикла, но в любом случае эти отклонения должны быть чем-то ограничены. В худшем случае рекомендуется, чтобы частота вызова цикла управления не отклонялась более чем на 20% на каждом участке из 10 вызовов. Иногда лучше пропустить часть значений, чтобы сохранить требуемую частоту вызова управляющего цикла. Однако несмотря на это я для ПИ-контроллера предпочитаю системы, в которых точность вызова цикла управления лежит в пределах 1-5%.
Если вашему контроллеру требуется значительно изменить состояние управлямой системы, которе не может быть произведено за короткое время - тогда всё это время отклонение будет велико и это огромное отклонение накопится в состоянии интегратора, что вызовет в свою очередь вызовет его "вылетание". Когда система достигнет своего целевого положения в интеграторе будет находится огромное накопленное отклонение, которое вызовете дальнейший значительный "перелёт" через требуемое положение и система так же значительное время будет продолжать двигаться уже за пределами целевого значения. В лучшем случае это будут затухающие колебания, в худшем - система никогда не стабилизируется и будет осциллировать с огромной амплитудой.
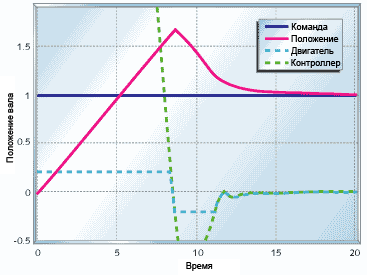
Рисунок 15. "Вылетание" пропорционально-интегрального управления
Рисунок 15 показывает эффект "вылетания" интегратора. Я использовал двигатель с редуктором и контроллер с примера рисунка 13 и ограничил скорость мотора до 0.2. Не только контроллер выдаёт управляющий сигнал, который не может быть реализован двигателем, но и вся система показывает значительный "перелёт". Реально требуемое положение достигается за 5 секунд, он обратный сигнал не подаётся еще в течение 3 секунд, поскольку в интеграторе еще осталось накопленное отклонение, указывающее на то, что надо продолжать двигаться вперёд, и проходит порядка 15 секунд, пока система не стабилизируется.
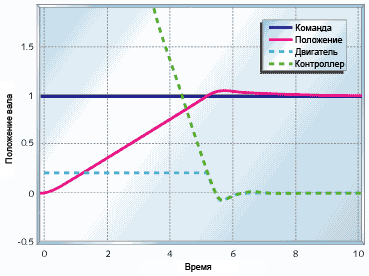
Рисунок 16. Ограничение "вылетания" пропорционально-интегрального управления
Простейший и самый прямой способ борьбы с "вылетанием" интегратора это установка ограничений на его накопленное значение, как я показал в примере кодирования такого интегратора. Рисунок 16 показывает что происходит когда в приведенных выше условиях на интегратор наложены ограничения в размере максимально допустимого управляющего воздействия на двигатель (iMin=-0.2, iMax=0.2). Выход контроллера всё еще больше допустимого для двигателя (из-за пропорциональной части), но теперь интегратор "вылетает" значительно меньше и система начинает стабилизироваться на 5-й секунде и заканчивает примерно на 6-й секунде.
Обратите внимание, что в примерах указанных выше надо масштабировать iMin и iMax, если вы изменяете коэффициент интегратора (iGain). Обычно достаточно установить ограничения значиний минимума и максимума интегратора такие, чтобы интегрирующий компонент управления выдавал соответственно минимальное и максимальное управляющее воздействие. Если вы знаете, что вам потребуется еще более малые интегрирующий компонент - вы можете еще больше ограничить значения интегратора.
Дифференциальное управление
Я не стал рассматривать сверхточное позиционирование в предыдущем разделе по той причине, что эту систему нельзя стабилизировать с помощью ПИ-управления. В общем если вы не можете стабилизировать какую-то систему с помощью пропорционального управления из-за слишком большой задержки воздействия на систему, тогда при использовании ПИ-управления увеличивающего эту задержку всё станет только хуже.
Мы знаем что пропорциональное управление соответствует использованию "сиюминутной" информации о системе, интегральное управление использует информацию о "прошлом" системы. Если бы мы получили элемент который соответствует использованию "прогнозной" информации о системе, мы смогли бы попробовать использовать его для стабилизации нашей платформы в системе сверхточного позиционирования. И таким искомым элементом является дифференциатор.
Код приведенный ниже показывает, как рассчитывается дифференциальная компонента ПИД-контроллера. Я предпочитаю использовать текущее состояние системы, а не отклонение от требуемого положения для мягкости управления при резкой смене целевого состояния системы. Дифференциальная компонента сама по себе представляет разность между предыдущим состоянием системы и текущим её состоянием. Это даёт нам возможность оценить скорость изменения состояния системы и предугадать в каком состоянии окажется система в следующий момент времени.
<source lang="c"> double dTerm;
. . .
dTerm = pid->dGain * (position - pid->dState);
pid->dState = position; . . .
</source>
При использовании дифференциальной компоненты становится возможным стабилизация платформы в системе сверхточного позиционирования.
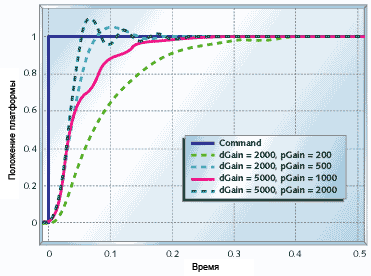
Рисунок 17. Пропорционально-дифференциальное управление системой сверхточного позиционирования
Рисунок 17 показывает как ведёт себя эта система под пропорционально-дифференциальным (ПД) управлением. Система стабилизируется меньше чем за 1/2 секунды по сравнению с несколькими секундами требующимися для других систем.
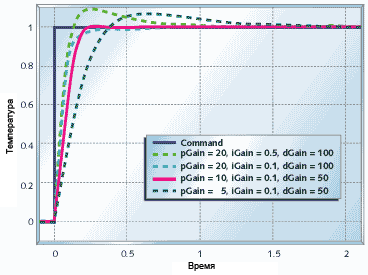
Рисунок 18. ПИД-управление термосистемой
Рисунок 18 показывает как себя ведёт термосистема под ПИД-управлением. Как видно из графиков этот подход существенно улучшает качество управления системой.
Дифференциальная компонента управления очень мощная, но она же и самая проблемная из всех типов управления представленных здесь. Три проблемы с которыми придётся столкнуться при реализации этого типа управления - нерегулярность частоты сбора данных, шумы и высокочастотные колебания. Когда я представлял код для дифференциального элемента я предположил, что выход управляющего воздействия должен быть пропорционален изменению положения деленному на время между итерациями цикла управления. Если состояние системы меняется с постоянной скорость, а время между запуском управляющей итерации варьируется, вы будете получать неверную информацию о скорости системы. Поскольку обычно время между итерациями управления достаточно мало, шумы такого сорта могут быть очень значительными и будут сильно мешать задаче управления.
Когда вы используете дифференциальное управление нужно обращать внимание на точность временных интервалов между итерациями управляющего цикла. Я рекомендую поддерживать точность этих интервалов в пределах 1%, однако чем точнее, тем лучше. Если вы не можете обеспечить это на аппаратном уровне - постарайтесь сделать это на уровне программного обеспечения, отдав под задачу сбора информации максимальный приоритет (не нужно с такой точностью выполнять расчеты управляющего воздействия, достаточно собирать информацию в нужные моменты времени). Один из оптимальных вариантов - поместить сбор информации о системе в прерывание, а сами расчеты ПИД-алгоритма выполнять в свободное время.
Дифференциальное управление страдает от шумов больше других типов управления потому что оно эти шумы усиливает, в отличие от пропорционального управления, которое просто транслирует эти шумы или интегрального, которое вообще шумы подавляет. Посмотрите на коэффициенты дифференциальной компоненыт, которые я использовал выше и представьте, что произойдёт если у вас в системе будут небольшие шумы, которые возникать при каждом получении информации о системе. Умножьте эти небольшие шумы на коэффициент 2000 и представьте как это отразится на системе.
Вы можете применить фильтрацию дифференциальной компоненты управления, но это существенно снизит её полезность. Теория стоящая за тем, как это делать и как опредилить - будет ли это работать останется за рамками этой вводной статьи. Возможно лучшее, что вы можете сделать с этой проблемой - is to look at how likely you are to see any noise, how much it will cost to get quiet inputs, and how badly you need the high performance that you get from differential control. Once you've worked this out, you can avoid differential control altogether, talk your hardware folks into getting you a lower noise input, or look for a control systems expert.
The full text of the PID controller code is shown in Listing 1 and is available at www.embedded.com/code.html.
Listing 1: PID controller code
<source lang="c"> typedef struct {
double dState; // Last position input
double iState; // Integrator state
double iMax, iMin;
// Maximum and minimum allowable integrator state
double iGain, // integral gain
pGain, // proportional gain
dGain; // derivative gain
} SPid; double UpdatePID(SPid * pid, double error, double position) {
double pTerm, dTerm, iTerm; pTerm = pid->pGain * error; // calculate the proportional term
// calculate the integral state with appropriate limiting
pid->iState += error; if (pid->iState > pid->iMax) pid->iState = pid->iMax; else if (pid->iState
<
pid->iMin) pid->iState = pid->iMin; iTerm = pid->iGain * iState; // calculate the integral term dTerm = pid->dGain * (position - pid->dState); pid->dState = position; return pTerm + iTerm - dTerm;
} </source>
Tuning
The nice thing about tuning a PID controller is that you don't need to have a good understanding of formal control theory to do a fairly good job of it. About 90% of the closed-loop controller applications in the world do very well indeed with a controller that is only tuned fairly well.
If you can, hook your system up to some test equipment, or write in some debug code to allow you to look at the appropriate variables. If your system is slow enough you can spit the appropriate variables out on a serial port and graph them with a spreadsheet. You want to be able to look at the drive output and the plant output. In addition, you want to be able to apply some sort of a square-wave signal to the command input of your system. It is fairly easy to write some test code that will generate a suitable test command. Once you get the setup ready, set all gains to zero. If you suspect that you will not need differential control (like the motor and gear example or the thermal system) then skip down to the section that discusses tuning the proportional gain. Otherwise start by adjusting your differential gain.
The way the controller is coded you cannot use differential control alone. Set your proportional gain to some small value (one or less). Check to see how the system works. If it oscillates with proportional gain you should be able to cure it with differential gain. Start with about 100 times more differential gain than proportional gain. Watch your drive signal. Now start increasing the differential gain until you see oscillation, excessive noise, or excessive (more than 50%) overshoot on the drive or plant output. Note that the oscillation from too much differential gain is much faster than the oscillation from not enough. I like to push the gain up until the system is on the verge of oscillation then back the gain off by a factor of two or four. Make sure the drive signal still looks good. At this point your system will probably be responding very sluggishly, so it's time to tune the proportional and integral gains.
If it isn't set already, set the proportional gain to a starting value between 1 and 100. Your system will probably either show terribly slow performance or it will oscillate. If you see oscillation, drop the proportional gain by factors of eight or 10 until the oscillation stops. If you don't see oscillation, increase the proportional gain by factors of eight or 10 until you start seeing oscillation or excessive overshoot. As with the differential controller, I usually tune right up to the point of too much overshoot then reduce the gain by a factor of two or four. Once you are close, fine tune the proportional gain by factors of two until you like what you see.
Once you have your proportional gain set, start increasing integral gain. Your starting values will probably be from 0.0001 to 0.01. Here again, you want to find the range of integral gain that gives you reasonably fast performance without too much overshoot and without being too close to oscillation.
Other issues
Unless you are working on a project with very critical performance parameters you can often get by with control gains that are within a factor of two of the "correct" value. This means that you can do all your "multiplies" with shifts. This can be very handy when you're working with a slow processor.
Sampling rate
So far I've only talked about sample rates in terms of how consistent they need to be, but I haven't told you how to decide ahead of time what the sample rate needs to be. If your sampling rate is too low you may not be able to achieve the performance you want, because of the added delay of the sampling. If your sampling rate is too high you will create problems with noise in your differentiator and overflow in your integrator.
The rule of thumb for digital control systems is that the sample time should be between 1/10th and 1/100th of the desired system settling time. System settling time is the amount of time from the moment the drive comes out of saturation until the control system has effectively settled out. If you look at Figure 16, the controller comes out of saturation at about 5.2s, and has settled out at around 6.2s. If you can live with the one second settling time you could get away with a sampling rate as low as 10Hz.
You should treat the sampling rate as a flexible quantity. Anything that might make the control problem more difficult would indicate that you should raise the sampling rate. Factors such as having a difficult plant to control, or needing differential control, or needing very precise control would all indicate raising the sampling rate. If you have a very easy control problem you could get away with lowering the sampling rate somewhat (I would hesitate to lengthen the sample time to more than one-fifth of the desired settling time). If you aren't using a differentiator and you are careful about using enough bits in your integrator you can get away with sampling rates 1,000 times faster than the intended settling time.
Exert control
This covers the basics of implementing and tuning PID controllers. With this information, you should be able to attack the next control problem that comes your way and get it under control.
Tim Wescott has a master's degree in electrical engineering and has been working in industry for more than a decade. His experience has included a number of control loops closed in software using 8- to 32-bit microprocessors, DSPs, assembly language, C, and C++. He is currently involved in control systems design at FLIR Systems where he specifies mechanical, electrical, and software requirements and does electrical and software design. You can contact him at tim@wescottdesign.com.